A ray tracer emits a ray from each pixel toward the scene to determine the color of the pixel, the process of computing the color can be split in three parts
- ray generation, the origin and direction of each pixel ray is computed
- ray intersection, the ray finds the closest object intersecting the viewing ray
- shading, where the intersection point, surface normal and other information is used to determine the color of the pixel
A ray can be represented with a 3D parametric line from the eye
Note that
- if
- if
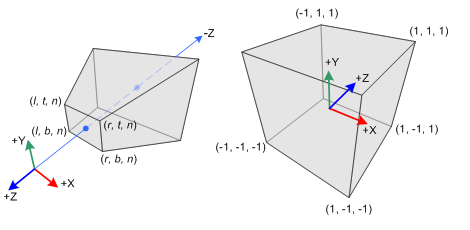
Camera coordinate system
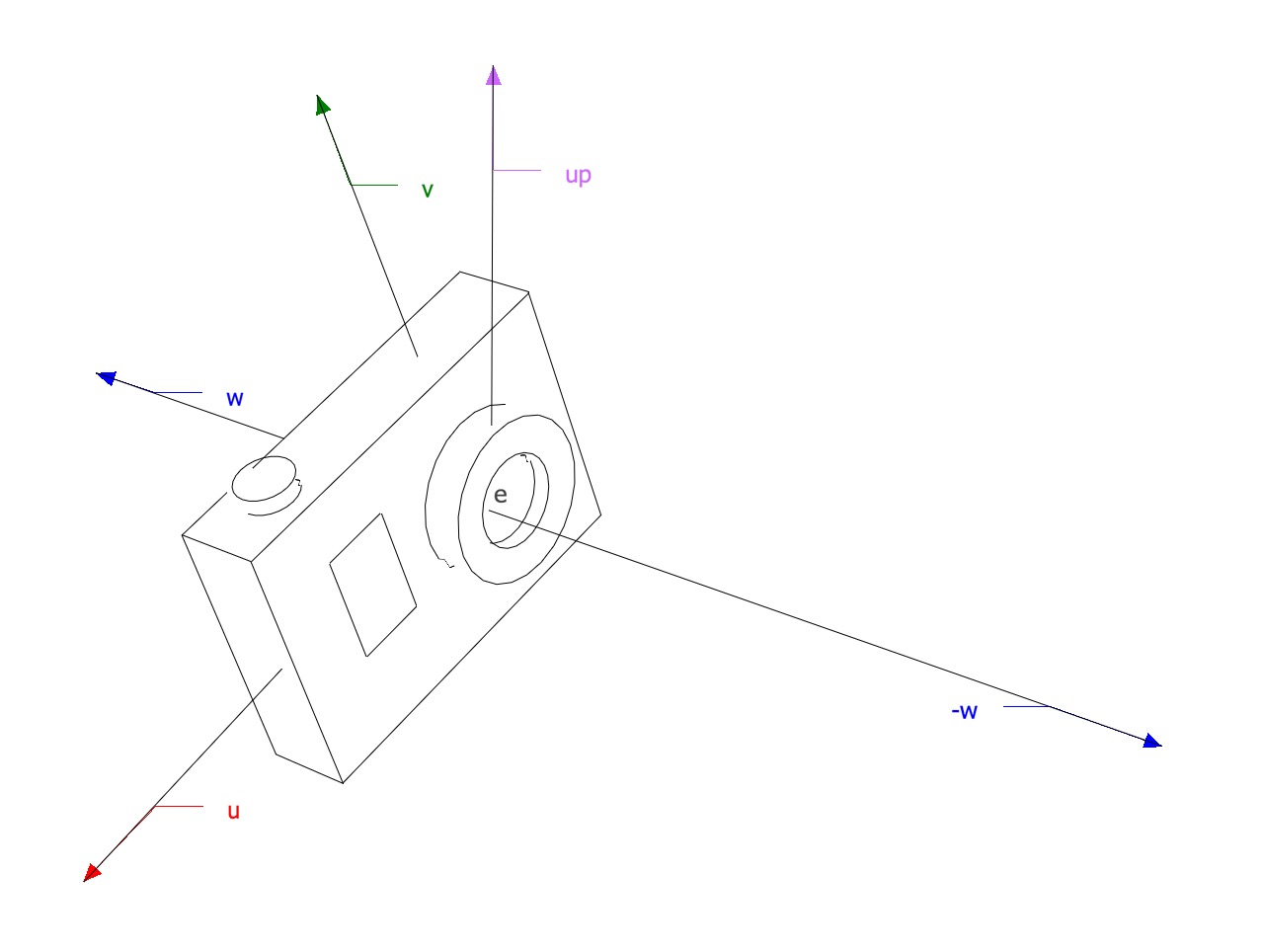
All the rays start from the origin of an orthonormal coordinate frame known as the camera/eye coordinate system, in this frame the camera is looking at the negative
camera
The coordinate system is built from
- the viewpoint
- the view direction which is
- the up vector which is used to construct a basis that has
Ray generation
Pixel coordinates
The image dimensions is defined with four numbers
Note that the coordinates are expressed in the camera coordinate frame defined in a plane parallel to the
The image has to be fitted within a rectangle of
Orthographic view
For an orthographic view all the rays will have the direction
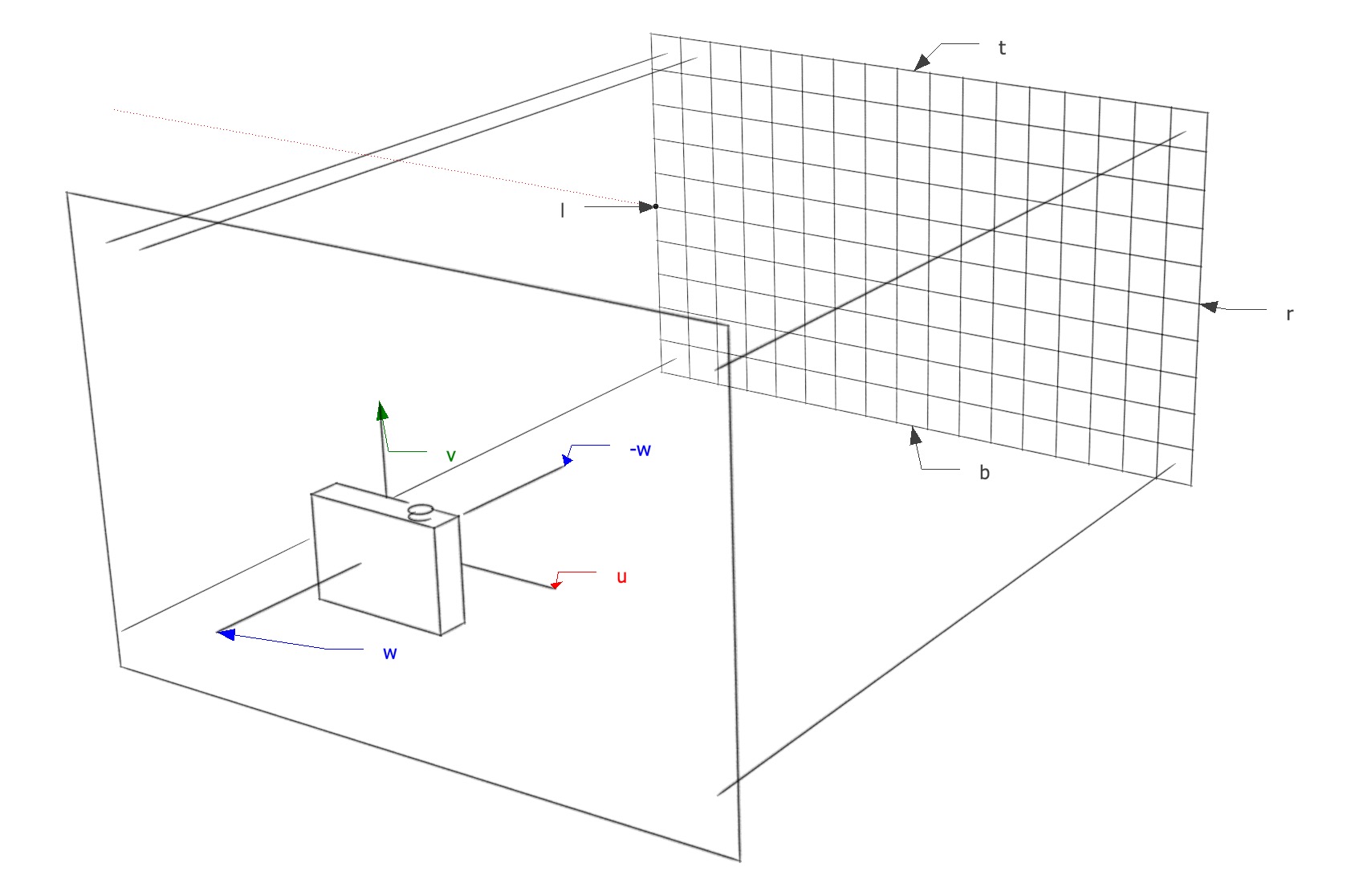
orthographic view
Perspective view
For a perspective view all the rays will have the same origin
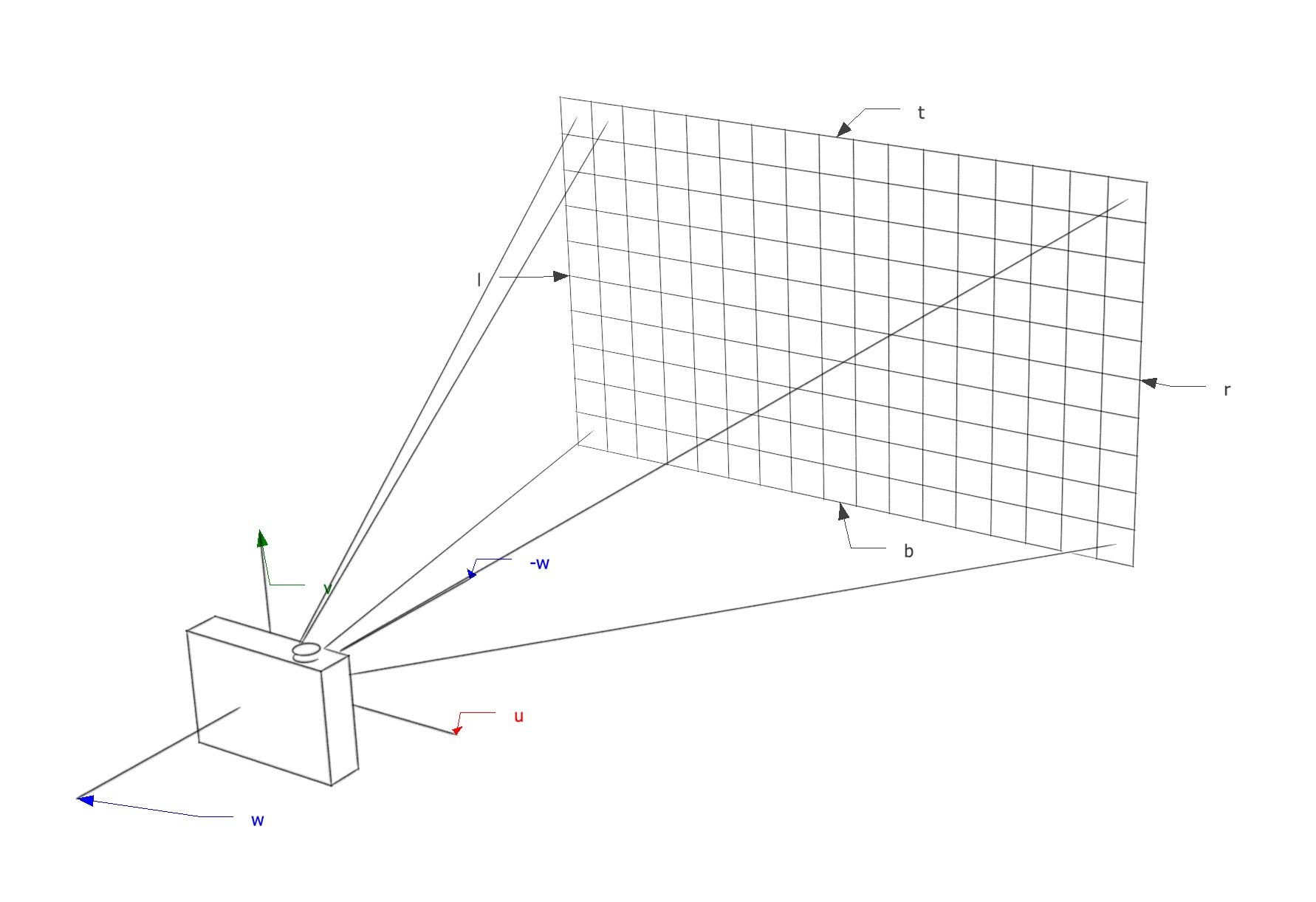
perspective view
Ray intersection
Once a ray in the form
The following pseudocode tests for “hits”
ray = e + td
t = infinity
for each `object` in the scene
if `object` is hit by `ray` and `ray's t` < `t`
hit object = `object`
t = `ray's t`
return hit t < infinity
Shading
Once the visible surface is known the next step is to compute the value of the pixel using a shading model, which can be made out of simple heuristics or elaborate numeric computations
A shading model is designed to capture the process of light reflection on a surface, the important variables in this process are
- other characteristics of the light source and the surface depending on the shading model
Lambertian shading
One of the simplest shading models discovered by Lambert in the 18th century, the amount of energy from a light source that falls on a surface depends on the angle of the surface to the light
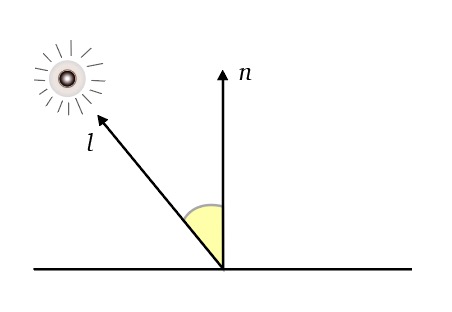
lambert
- A surface facing directly the light receives maximum illumination
- A surface tangent to the light receives no illumination
- A surface facing away from the light receives no illumination
Thus the illumination is proportional to the cosine of the angle between
Where
Additional notes of this model
- The model is view independent
- The color of the surface appears to have a very matte, chalky appearance
Blinn-Phong shading
Many surfaces show some degree of highlights (shininess) or specular reflections that appear to move as the viewpoint changes, the idea is to produce reflections when
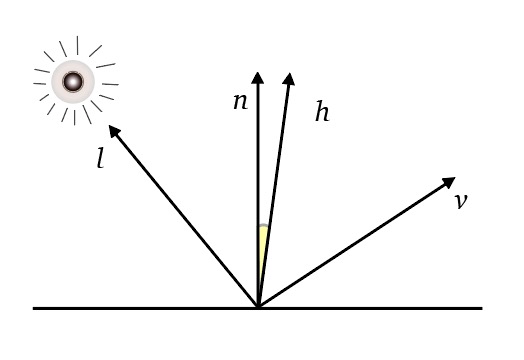
blinn phong
- the half vector
Also
- if
- the specular component decreases exponentially when
The color of the pixel is then
Where
Note that the color of the pixel is the overall contribution of both the lambertian shading model and the blinn-phong shading model
Ambient shading
Surfaces that receive no illumination are rendered completely black, to avoid this a constant component is added to the shading model, the color depends entirely on the object hit with no dependence on the surface geometry
Where