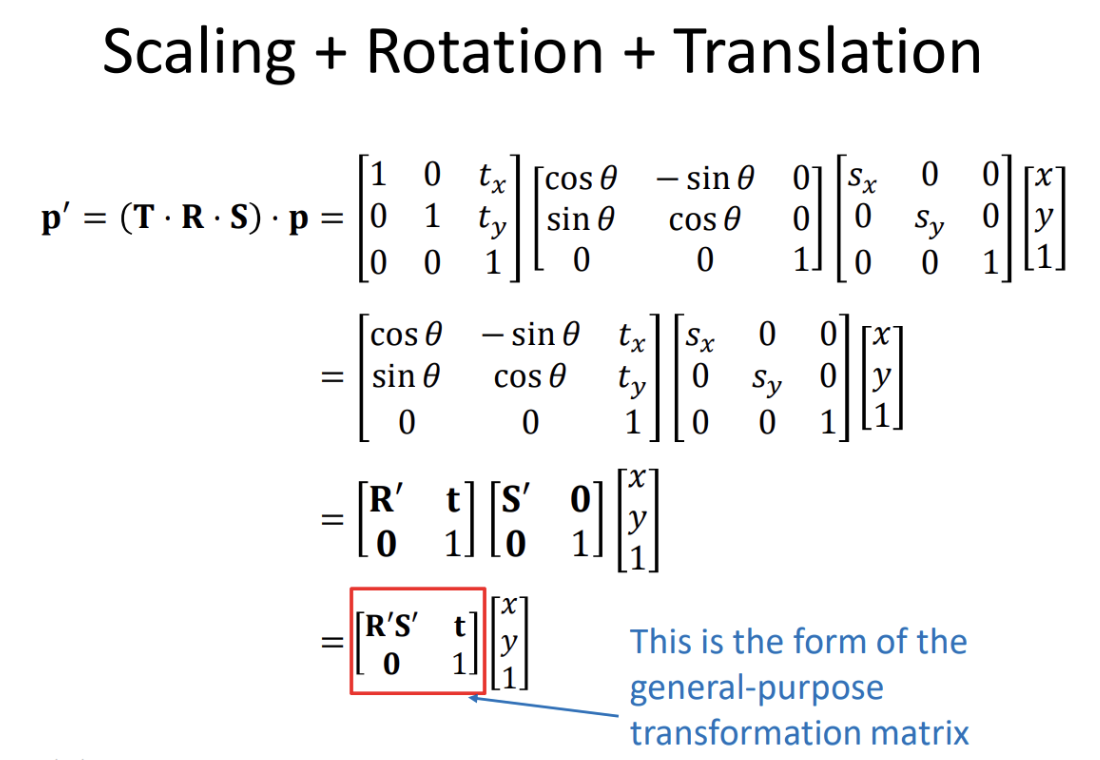
We can compose a series of transformations by multiplying the matrices that define the transformation, for example if we have one object in the world with arbitrary position and orientation that we want to render through a camera lens located in the same world also with arbitrary position and orientation, to get the coordinates of the object relative to the camera lens we must transform the object from object space to world space (transformation known as model transform) denoted by the matrix $\mathbf{M}_{world \leftarrow object}$, and then transform the vertices of the object from world space to view space (transformation known as view transform) denoted with $\mathbf{M}_{view \leftarrow world}$

$$ \begin{align*} \mathbf{v}_{world} &= \mathbf{M}_{world \leftarrow object} \mathbf{v}_{object} \\ \mathbf{v}_{view} &= \mathbf{M}_{view \leftarrow world} \mathbf{v}_{world} \\ &= \mathbf{M}_{view \leftarrow world} \mathbf{M}_{world \leftarrow object} \mathbf{v}_{object} \end{align*} $$

We can associate the transformation matrices and have a single matrix to transform vertices of the object directly to camera space

$$ \begin{align*} \mathbf{v}_{view} &= (\mathbf{M}_{view \leftarrow world} \mathbf{M}_{world \leftarrow object})\mathbf{v}_{object} \\ &= \mathbf{M}_{view \leftarrow object} \mathbf{v}_{object} \end{align*} $$

Now if we have two transformation matrices $\mathbf{M}$ and $\mathbf{N}$ and they are applied to some vector $\mathbf{v}$ in that respective order their product is

$$ \begin{align*} \mathbf{NM} = \begin{bmatrix} \mathbf{\cuv{s}} & \mathbf{\cuv{t}} & \mathbf{\cuv{u}} \end{bmatrix} \begin{bmatrix} \mathbf{\cuv{p}} & \mathbf{\cuv{q}} & \mathbf{\cuv{r}} \end{bmatrix} = \begin{bmatrix} p_x \mathbf{s} + p_y \mathbf{t} + p_z \mathbf{u} \\ q_x \mathbf{s} + q_y \mathbf{t} + q_z \mathbf{u} \\ r_x \mathbf{s} + r_y \mathbf{t} + r_z \mathbf{u} \\ \end{bmatrix}^T \end{align*} $$

We can see that the rows of the product $\mathbf{NM}$ are the result of transforming the basis vectors of $\mathbf{M}$ by the transformation matrix $\mathbf{N}$ so matrix-matrix multiplication encodes a basis vectors transformation

Rotation followed by translation

Given the vector $\mathbf{v}$ let’s apply a rotation and a translation transform in that order

$$ \mathbf{v'} = \mathbf{TRv} $$

Let’s analyze the product $\mathbf{TR}$

$$ \mathbf{TR} = \begin{bmatrix} I_{3 \times 3} & T_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} R_{3 \times 3} & 0_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{bmatrix} = \begin{bmatrix} R_{3 \times 3} & T_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{bmatrix} $$

Which when multiplied by $\mathbf{v}$ results in

$$ \mathbf{v'} = \mathbf{TRv} = \begin{bmatrix} R_{3 \times 3} & T_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} \mathbf{v}_{3 \times 1} \\ 1 \end{bmatrix} = \begin{bmatrix} R_{3 \times 3} \mathbf{v}_{3 \times 1} + T_{3 \times 1} \\ 1 \end{bmatrix} $$

$\mathbf{v’}$ will have a compact form equal to

$$ \mathbf{v'} = \mathbf{TRv} = \mathbf{Rv} + T_{3 \times 1} $$

Translation followed by rotation

Given the vector $\mathbf{v}$ let’s apply a translation and a rotation transform in that order

$$ \mathbf{v'} = \mathbf{RTv} $$

Let’s analyze the produce $\mathbf{RT}$

$$ \mathbf{RT} = \begin{bmatrix} R_{3 \times 3} & 0_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} I_{3 \times 3} & T_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{bmatrix} = \begin{bmatrix} R_{3 \times 3} & R_{3 \times 3} T_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{bmatrix} $$

Which when multiplied by $\mathbf{v}$ results in

$$ \mathbf{v'} = \mathbf{TRv} = \begin{bmatrix} R_{3 \times 3} & R_{3 \times 3} T_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{bmatrix} \begin{bmatrix} \mathbf{v}_{3 \times 1} \\ 1 \end{bmatrix} = \begin{bmatrix} R_{3 \times 3} \mathbf{v}_{3 \times 1} + R_{3 \times 3} T_{3 \times 1} \\ 1 \end{bmatrix} $$

$\mathbf{v’}$ will have a compact form equal to

$$ \mathbf{v'} = \mathbf{RTv} = \mathbf{Rv} + \mathbf{R}T_{3 \times 1} $$

Note that both the vector $\mathbf{v}$ and the translation vector are transformed by $\mathbf{R}$

Transformations between coordinate systems

The following figure shows two coordinate system, the one with the basis vectors $\mathbf{x}, \mathbf{y}$ and $\mathbf{z}$ is the canonical coordinate system, $\mathbf{u}, \mathbf{v}$ and $\mathbf{w}$ are the basis of a nested coordinate system expressed in terms of the canonical coordinate system

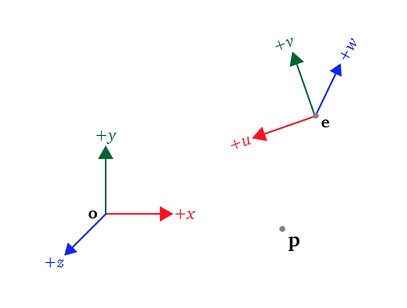
coordinate systems

coordinate systems

The value of $\mathbf{p}$ expressed in the canonical coordinate system is

$$ \mathbf{p} = x_p \mathbf{x} + y_p \mathbf{y} + z_p \mathbf{z} $$

Similarly we can express $\mathbf{p}$ with the following equation

$$ \mathbf{p} = \mathbf{e} + u_p \mathbf{u} + v_p \mathbf{v} + w_p \mathbf{w} $$

Note that both equations express $\mathbf{p}$ in terms of the canonical coordinate system, we can express the same relationship using transformations matrices as a rotation followed by a translation

$$ \begin{bmatrix} x_p \\ y_p \\ z_p \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & x_e \\ 0 & 1 & 0 & y_e \\ 0 & 0 & 1 & z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_u & x_v & x_w & 0 \\ y_u & y_v & y_w & 0 \\ z_u & z_v & z_w & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} u_p \\ v_p \\ w_p \\ 1 \end{bmatrix} \\ \begin{bmatrix} x_p \\ y_p \\ z_p \\ 1 \end{bmatrix} = \begin{bmatrix} x_u & x_v & x_w & x_e \\ y_u & y_v & y_w & y_e \\ z_u & z_v & z_w & z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} u_p \\ v_p \\ w_p \\ 1 \end{bmatrix} $$

We can then introduce $\mathbf{p}_{uvw}$ which is the point $\mathbf{p}$ expressed in the nested coordinate system, similarly $\mathbf{p}_{xyz}$ is the same point expressed in canonical coordinate system

$$ \begin{equation} \label{frame-to-canonical} \mathbf{p}_{xyz} = \begin{bmatrix} \mathbf{u}_{3 \times 1} & \mathbf{v}_{3 \times 1} & \mathbf{w}_{3 \times 1} & \mathbf{e}_{3 \times 1} \\ 0 & 0 & 0 & 1 \end{bmatrix} \mathbf{p}_{uvw} \end{equation} $$

This is the frame-to-canonical transformation matrix for the $(u,v,w)$ coordinate space

The inverse transformation is given by a translation followed by a rotation

$$ \begin{bmatrix} u_p \\ v_p \\ w_p \\ 1 \end{bmatrix} = \begin{bmatrix} x_u & y_u & z_u & 0 \\ x_v & y_v & z_v & 0 \\ x_w & y_w & z_w & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_p \\ y_p \\ z_p \\ 1 \end{bmatrix} $$

Which is the same as finding the value of $\mathbf{p}_{uvw}$ in \eqref{frame-to-canonical}

$$ \mathbf{p}_{uvw} = \begin{bmatrix} \mathbf{u}_{3 \times 1} & \mathbf{v}_{3 \times 1} & \mathbf{w}_{3 \times 1} & \mathbf{e}_{3 \times 1} \\ 0 & 0 & 0 & 1 \end{bmatrix}^{-1} \mathbf{p}_{xyz} $$

This is the canonical-to-frame transformation matrix for the $(u,v,w)$ coordinate space

References

  • Dunn, F. and Parberry, I. (2002). 3D math primer for graphics and game development. Plano, Tex.: Wordware Pub.