Coordinate systems and transformations between them

This article is part 1 in the series about transformation matrices:

World space¹, upright space, object space

why bother having multiple spaces?

Information is given only in the context of a particular reference frame

world space: global reference frame
- the position of other coordinates spaces can be expressed in terms of this space
- this space cannot be expressed in terms of any larger/outer space
- note that there’s no “absolute” space however this space is the largest one we care about
object space: space associated with each object that belongs to the world space
- camera space: object space associated with the viewport used for rendering
upright space: special space associated with each object, it’s halfway between world space and object space in the sense that the axes of this space are parallel to the ones of the world space but the origin of this space is coincident with the origin of the object space

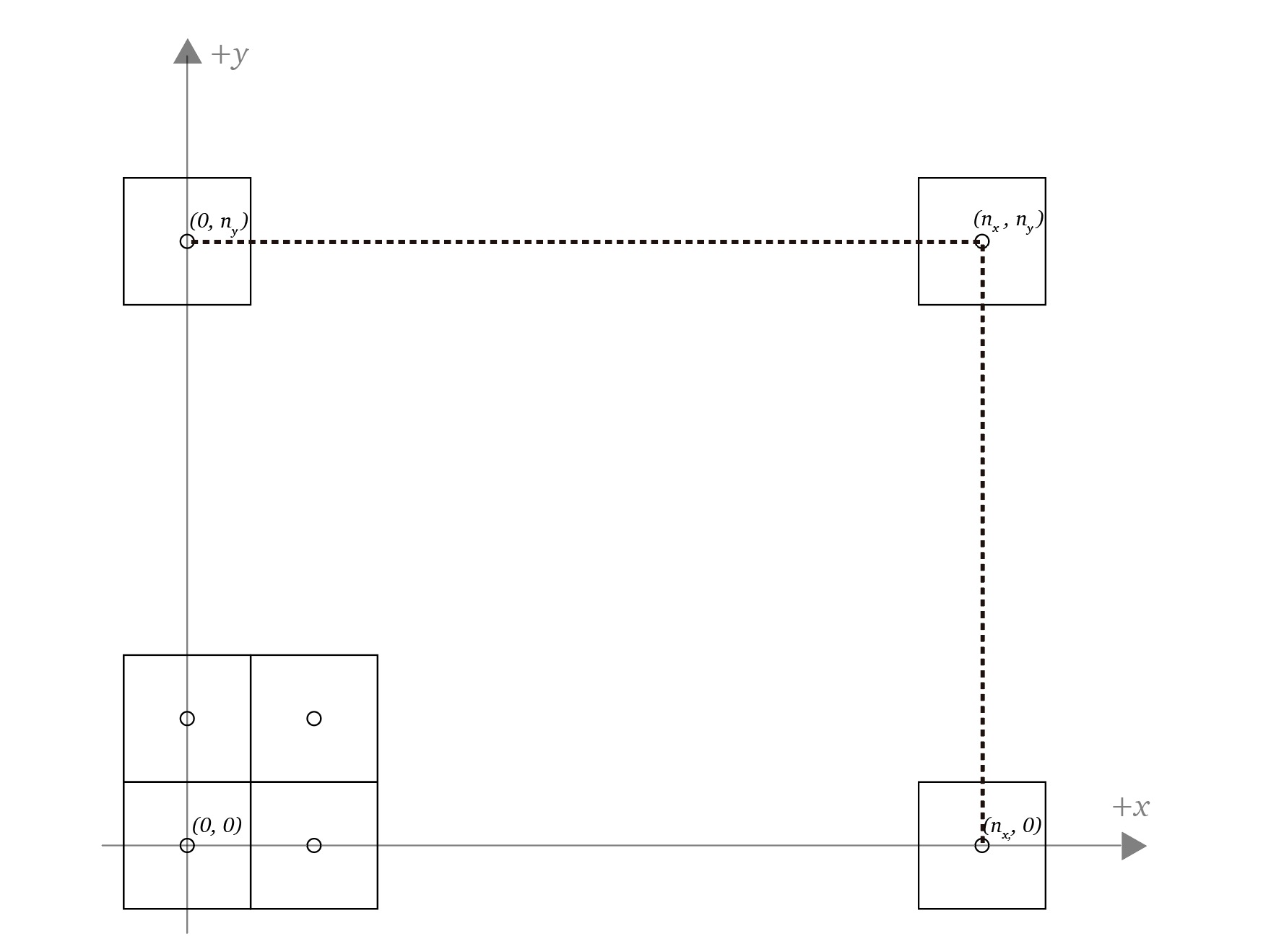
Why do we have an upright space?

Thanks to this space the problem of transforming a point between object space -> world space (and vice-versa) can be divided in two subproblems

object space -> upright space (a rotation)
upright space -> world space (a change of location)

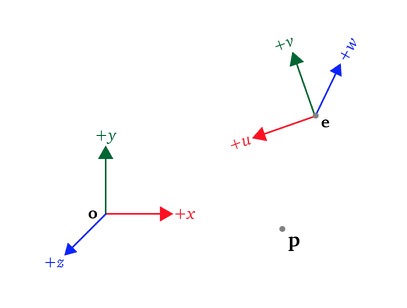
Coordinates of a vector

A coordinate system consists of

an origin (displacement from another coordinate system origin)
a basis (a set of three vectors)

The numeric coordinates of a vector expressed with respect to some basis are the coefficients of the representation of the vector as a linear combination of the basis

v = v_{x} i + v_{y} j + v_{z} k

In other words the numeric coordinates are the quantities that multiply each basis vector which are $v_{x}$ , $v_{y}$ and $v_{z}$

When the basis vectors are $i = [1, 0, 0]$ , $j = [0, 1, 0]$ and $k = [0, 0, 1]$ then

\begin{aligned} v & = v_{x} [\begin{array}{c} 1 & 0 & 0 \end{array}] + v_{y} [\begin{array}{c} 0 & 1 & 0 \end{array}] + v_{z} [\begin{array}{c} 0 & 0 & 1 \end{array}] \\ = [\begin{array}{c} v_{x} & v_{y} & v_{z} \end{array}] \end{aligned}

Transformations between space coordinates

From object space to upright space

Let $v$ be some vector expressed/measured relative to a space (object space) whose basis vectors are $p, q, r$ (which are themselves expressed/measured relative to a wrapper space), the vector $v$ expressed relative to the wrapper space is

\begin{aligned} (1) & v_{u p r i g h t} & = v_{x} p + v_{y} q + v_{z} r \\ = v_{x} [\begin{array}{c} p_{x} & p_{y} & p_{z} \end{array}] + v_{y} [\begin{array}{c} q_{x} & q_{y} & q_{z} \end{array}] + v_{z} [\begin{array}{c} r_{x} & r_{y} & r_{z} \end{array}] \\ = [\begin{array}{c} v_{x} p_{x} + v_{y} q_{x} + v_{z} r_{x} & v_{x} p_{y} + v_{y} q_{y} + v_{z} r_{y} & v_{x} p_{z} + v_{y} q_{z} + v_{z} r_{z} \end{array}] \end{aligned}

Note that if $p, q, r$ were not orthogonal then $v_{u p r i g h t}$ couldn’t be uniquely determined

The coordinates of $p, q, r$ are always equal to $[1, 0, 0], [0, 1, 0]$ and $[0, 0, 1]$ respectively when expressed using the coordinate system for which they are the basis, relative to other wrapper coordinate systems they will have arbitrary coordinates

From upright space to world space

Since the axes of the upright space are parallel to the axes of the world space the only difference between these spaces is the translation of these axes with respect to the origin of the axes of the world space, let $o$ be the translation of the upright basis axes then

v_{w o r l d} = o + v_{u p r i g h t}

From world space to upright space

We just have to translate the whole space so that the origin lies exactly on the origin of the upright space, if $o$ is the origin of the upright space expressed in world space then

v_{u p r i g h t} = v_{w o r l d} - o

From upright space to object space

What if $v_{u p r i g h t}$ is known and we want to know $v$ ? The dot product is the key as it’s used to measure distance in a particular direction, since we know that the basis vectors $p, q, r$ are expressed in terms of the upright space perspective we just have to calculate the projection of $v_{u p r i g h t}$ in the direction of each $p, q, r$

\begin{array}{r} v_{x} = v_{u p r i g h t} \cdot p \\ v_{y} = v_{u p r i g h t} \cdot q \\ v_{z} = v_{u p r i g h t} \cdot r \end{array}

If we use $(1)$ this works because the dot product with $p$ will isolate the $v_{x}$ coordinate

\begin{aligned} v_{u p r i g h t} \cdot p & = v_{x} (p \cdot p) + v_{y} (q \cdot p) + v_{z} (r \cdot p) \\ = v_{x} (1) + v_{y} (0) + v_{z} (0) \\ = v_{x} \end{aligned}

Note: this only works when $p, q, r$ are orthonormal, for the general case we have to solve this using linear algebra

words like “coordinate system”, “coordinate frame” or “space” are used interchangeably ↩︎