Translating objects with a Transformation Matrix

This article is part 4 in the series about transformation matrices:

2D translation

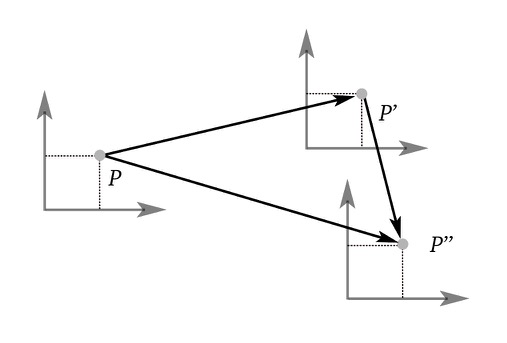
A translation is an affine transformation which is a linear transformation followed by some displacement

v^{'} = Mv + b

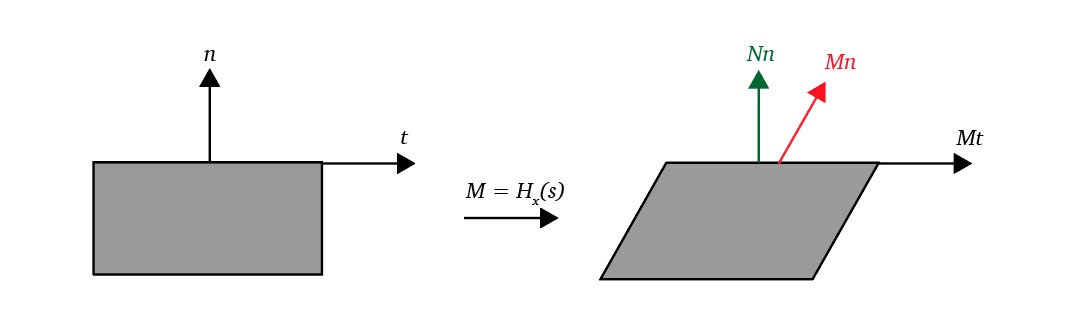
Even though we can’t express 2D translation using a 2x2 matrix, we can express such a transformation as a shearing transformation in 3D projective geometry , to do so we have to imagine that the 2D Euclidean world exists as the plane $w = 1$ in a 3D space, under this geometry any point has the form $[\begin{matrix} x & y & 1 \end{matrix}]$

In Euclidean geometry a vector expressed as a linear combination of the standard basis has the form

v = v_{x} \hat{i} + v_{y} \hat{j} = {[\begin{matrix} v_{x} & v_{y} \end{matrix}]}^{T}

In Projective geometry a vector which exists in the plane $w = 1$ has the form

v = v_{x} \hat{i} + v_{y} \hat{j} + 1 \hat{w} = {[\begin{matrix} v_{x} & v_{y} & 1 \end{matrix}]}^{T}

This basis can be represented using the following transformation matrix

M = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}] = [\begin{matrix} \overset{|}{\underset{|}{i}} & \overset{|}{\underset{|}{j}} & \overset{|}{\underset{|}{w}} \end{matrix}]

The translation transform then can be seen in Projective geometry as a simple shearing of the space by the coordinate $w$ , using the shearing transform $H_{xy} (Δ x, Δ y)$ to transform a point $v$

v^{'} = H_{xy} (Δ x, Δ y) v = [\begin{matrix} 1 & 0 & Δ x \\ 0 & 1 & Δ y \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \\ 1 \end{matrix}] = [\begin{matrix} v_{x} + Δ x \\ v_{y} + Δ y \\ 1 \end{matrix}]

Now that we’re using perspective geometry to represent entities, let’s imagine a point $p = [\begin{matrix} x & y & 0 \end{matrix}]$ (a point that lies in the plane $w = 0$ ), whenever this point is transformed by a transformation matrix we can notice that the translation components of the matrix are cancelled because of $w = 0$ , we can take advantage of this fact and represent vectors with this notation.

Let $v_{\infty}$ be a point located in the plane $w = 0$ , applying the shearing operation $H_{xy} (s, t)$ results in

v_{\infty}^{'} = H_{x y} (Δ x, Δ y) v_{\infty} = [\begin{matrix} 1 & 0 & Δ x \\ 0 & 1 & Δ y \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \\ 0 \end{matrix}] = [\begin{matrix} v_{x} \\ v_{y} \\ 0 \end{matrix}]

It’s important to note that this matrix multiplication is still a linear transformation and that this trick of translating 2D points is actually a shearing of the 3D projective plane

3D translation

Similarly to 2D a 3D translation can be represented as a shearing of the 4D projective hyperplane which has the form

T = H_{xyz} (Δ x, Δ y, Δ z) = [\begin{matrix} 1 & 0 & 0 & Δ x \\ 0 & 1 & 0 & Δ y \\ 0 & 0 & 1 & Δ z \\ 0 & 0 & 0 & 1 \end{matrix}]

When a 4D vector existing on the hyperplane $w = 1$ is transformed with this matrix the result is

v^{'} = H_{xyz} (Δ x, Δ y, Δ z) v = [\begin{matrix} 1 & 0 & 0 & Δ x \\ 0 & 1 & 0 & Δ y \\ 0 & 0 & 1 & Δ z \\ 0 & 0 & 0 & 1 \end{matrix}] [\begin{matrix} v_{x} \\ v_{y} \\ v_{z} \\ 1 \end{matrix}] = [\begin{matrix} v_{x} + Δ x \\ v_{y} + Δ y \\ v_{z} + Δ z \\ 1 \end{matrix}]

The general 3D translation matrix is then denoted as

\begin{matrix} (1) & T = [\begin{matrix} 1 & 0 & 0 & T_{x} \\ 0 & 1 & 0 & T_{y} \\ 0 & 0 & 1 & T_{z} \\ 0 & 0 & 0 & 1 \end{matrix}] = [\begin{matrix} I_{3 \times 3} & T_{3 \times 1} \\ 0_{1 \times 3} & 1 \end{matrix}] \end{matrix}