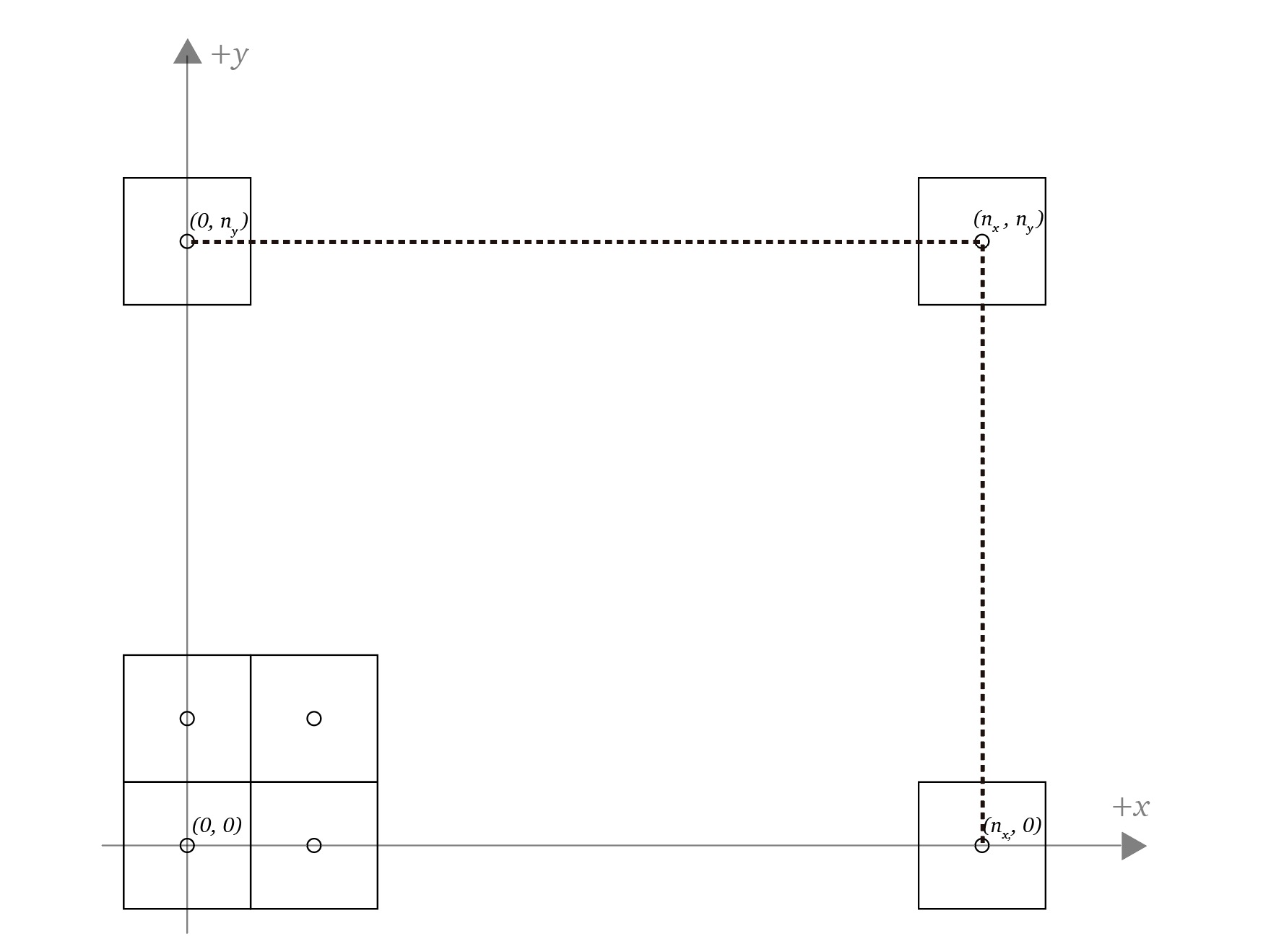
Transformation Matrix to Transform Objects from NDC Coordinates to Screen Coordinates (Viewport Transform)

One matrix transformation in the 3D to 2D transformation pipeline is the viewport transform, where objects are transformed from normalized device coordinates (NDC) to screen coordinates (SC).

In short, it's the transformation of numbers in the range [-1, 1] to numbers corresponding to pixels on the screen, which is a linear mapping computed with linear interpolation.
In this article, I cover the math behind the generation of the viewport transformation matrix.

Published on Tue, Mar 8, 2016
Last modified on Mon, Sep 8, 2025
288 words - Page Source

The objective of this step is to find a transformation matrix to transform points expressed in normalized device coordinates to screen coordinates.

v_{s c r e e n} = M_{v p} v_{n d c}

The canonical view volume needs to be mapped to the screen that has $n_{x} \times n_{y}$ pixels in a way so that points with $x = - 1$ and $x = 1$ are mapped to the left and right sides of the screen, respectively, and $y = - 1$ and $y = 1$ are mapped to the bottom and top sides of the screen, respectively. The $z$ -coordinate isn’t visible in a 2D image, so it can be discarded for the mapping.

Since the mapping is linear, we can use the linear interpolation method :

f (x) = o u t_{l o} + (o u t_{h i} - o u t_{l o}) \frac{x - i n_{l o}}{i n_{h i} - i n_{l o}}

Given:

$o u t_{l o} = - 0.5$
$o u t_{h i} = n_{x} - 0.5$
$i n_{l o} = - 1$
$i n_{h i} = 1$

The value of $x_{s c r e e n}$ is:

\begin{aligned} x_{s c r e e n} & = - 0.5 + n_{x} \frac{x_{n d c} + 1}{2} \\ = - \frac{1}{2} + \frac{n_{x}}{2} x_{n d c} + \frac{n_{x}}{2} \\ = \frac{n_{x}}{2} x_{n d c} + \frac{n_{x} - 1}{2} \end{aligned}

The value of $y_{s c r e e n}$ is found in a similar way:

y_{s c r e e n} = \frac{n_{y}}{2} y_{n d c} + \frac{n_{y} - 1}{2}

Finally, the transformation matrix that converts points from NDC to screen coordinates is:

M_{v p} = [\begin{matrix} \frac{n_{x}}{2} & 0 & 0 & \frac{n_{x} - 1}{2} \\ 0 & \frac{n_{y}}{2} & 0 & \frac{n_{y} - 1}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

Note that the $z$ -coordinate doesn’t need to be modified since it doesn’t affect the projection in the image. The $z$ -coordinate is still used to check the order in which objects should be drawn.

References

Transformation Matrix for Projection of 3D Objects into a 2D Plane (Projection Transform)

Transformation Matrix to Transform 3D Objects from World Space to View Space (View Transform)

Translating Objects with a Transformation Matrix