A first person camera captures objects from the viewpoint of a player’s character, the camera has the following characteristics:

• orbit: the character can look to the left, right, up & down, however if we imagine the head of the character it can’t be tilted
• translation: the character can move in 4 directions, forward backward, to the left and to the right, note that the vector that represents the direction the character is looking at doesn’t change (the orbit is not affected by translation)
  • our camera will always move in the same direction the camera is looking at, this is usually done differently on first person shooters where the character may move in a different direction than the direction the camera is looking at

Both characteristics can be implemented by creating a space for the camera and defining the direction in this space, that way translation doesn’t modify the direction the camera is looking at and for orbit we would rotate the basis vectors of the space

Assuming that the world space axes are as follows

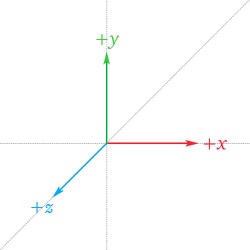
Let ${\mathbf{M}}_{upright\leftarrow camera}$ be the rotation matrix that transform points from camera space to upright space, also let the “look at” vector be defined as ${\mathbf{p}}_{camera}={\left[\begin{array}{ccc}0& 0& -1\end{array}\right]}^T$ in camera space. To define the rotation matrix ${\mathbf{M}}_{upright\leftarrow camera}$ let’s first identify the euler angles involved in the rotation, taking the image above as a reference we can identify the following actions:

• the character looks to the left or right - rotation relative to the upright space $y$-axis
• the character looks up or down - rotation relative to the upright space $x$-axis

Note that the sequence of intrinsic rotations $y-x^{\prime }$ or $x-y$ if expressed as a sequence of extrinsic rotations) represents the rotation of the camera, the sequence of extrinsic rotations can be represented as a multiplication of the following rotation matrices

The angles $\alpha$ and $\beta$ are computed as follows:

• let $\mathrm{\Delta }\alpha$ and $\mathrm{\Delta }\beta$ represent the change in the rotation around the $\mathbf{Y}$ and $\mathbf{X}$ axis respectively, the values of $\alpha$ and $\beta$ are computed based on the previous state

• if the character looks up then $\mathrm{\Delta }\beta$ is positive
• if the character looks to the right then $\mathrm{\Delta }\alpha$ is negative

Mouse coordinates delta to extrinsic rotations delta

Next we need to define what happens when we move the mouse, we can configure a window manager like GLFW to call a callback method whenever we move the mouse with the coordinates of the mouse as an argument (e.g. as $x_{new}$ and $y_{new}$), Note: the coordinates of the mouse are expressed relative to the top left corner of the window whose $+x$-axis points right and $+y$-axis points down, if we keep the old coordinates of the mouse (as $x_{old}$ and $y_{old}$) we can obtain how much the mouse moved with respect to the old position with the following calculation

Note that $y_{new}-y_{old}$ will be positive if we move the mouse down which is unintuitive, therefore we can multiply this result by $-1$ so that moving the mouse downward sets a negative value in $\mathrm{\Delta }y$

The next step is to update the values of $\alpha$ (yaw) and $\beta$ (pitch) using $\mathrm{\Delta }x$ and $\mathrm{\Delta }y$, note that when we move the mouse to the right we’re moving clockwise with respect to the $+y$ axis and when we move the mouse upward we’re moving counterclockwise with respect to the $+x$-axis therefore

Note that the we also need to value of $\beta$ to be inside the range $-{90}^{°}\le \beta \le {90}^{°}$ to avoid looking backwards

Finally to compute the value of ${\mathbf{p}}_{world}$ we need to transform ${\mathbf{p}}_{object}$ with ${\mathbf{M}}_{world\leftarrow object}$, note that the value of ${\mathbf{p}}_{object}={\left[\begin{array}{ccc}0& 0& -1\end{array}\right]}^T$ is always the same, therefore the value of ${\mathbf{p}}_{world}$ is

#pragma once

class FPS_Mouse {
public:
  float sensitivity;
  float yaw
  float pitch;
  glm::vec4 target;

  static const glm::vec3 YAW_AXIS = glm::vec3(0.0f, 1.0f, 0.0f);
  static const glm::vec3 PITCH_AXIS = glm::vec3(1.0f, 0.0f, 0.0f);

  FPS_Mouse(float yaw, float pitch);
  void process_mouse_movement(double delta_x, double delta_y, bool constraint_pitch);
  glm::mat4 get_view_matrix() const;

private:
  static const glm::vec4 P = glm::vec3(0.0f, 0.0f, -1.0f, 1.0f);
  void update_target();
}

FPS_Mouse::FPS_Mouse(float yaw = 0, float pitch = 0) :
    sensitivity(0.05f) {
  this->yaw = yaw;
  this->pitch = pitch;
  this->update_target();
}

void FPS_Mouse::process_mouse_movement(double delta_x, double delta_y, bool constraint_pitch = true) {
  yaw -= delta_x * sensitivity;
  pitch += delta_y * sensitivity;

  if (constraint_pitch) {
    if (pitch > 89.0f) { pitch = 89.0f; }
    if (pitch < -89.0f) { pitch = -89.0f; }
  } 
  this->update_target();
}

void FPS_Mouse::update_target() {
  /* Y = glm::rotate(glm::mat4(1.0f), glm::radians(yaw), FPS::YAW_AXIS); */
  /* X = glm::rotate(glm::mat4(1.0f), glm::radians(pitch), FPS::PITCH_AXIS); */
  /* target = Y * X * p; */
  float yaw_radians = glm::radians(yaw);
  float pitch_radians = glm::radians(pitch);
  target.x = -sin(yaw_radians) * cos(pitch_radians);
  target.y = sin(pitch_radians);
  target.z = -cos(yaw_radians) * cos(pitch_radians);
}