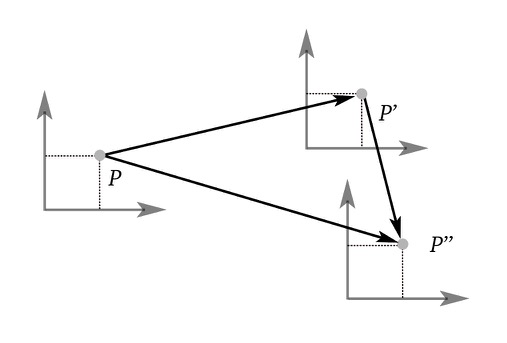
Image a vector space where two points $P$ and $P’$ exist, then there’s a unique translation of the plane that maps $P$ to $P’$ which means that the space of translations in the plane can be identified with a set of vectors that exist in the plane, composition of translation correspond to addition of vectors e.g. $\v{PP’’} = \v{PP’} + \v{P’P’’}$

affine space

affine space

An affine space is a space where translation is defined, formally an affine space is a set $E$ (of points) that admits a free transitive action of a vector space $\v{E}$ (of translations) whose action results in an element of the set $E$, that is there’s a map $E \times \v{E} \rightarrow E: (a,\mathbf{v}) \mapsto a + \mathbf{v}$ such that

  1. The zero vector acts as an identity i.e. for all $a \in E$, $a + \mathbf{0} = a$
  2. Addition of vectors correspond to translations i.e. for all $a \in E$ and $\mathbf{u,v} \in \v{E}$, $x + (\mathbf{u} + \mathbf{v}) = (x + \mathbf{u}) + \mathbf{v}$
  3. For any $a,b \in E$ there’s a unique free vector $\mathbf{u} \in \v{E}$ such that $a + \mathbf{u} = b$

The affine space is commonly represented with the triple $\left \langle E, \v{E}, + \right \rangle$ where $E$ is a set of points, $\v{E}$ a vector space acting on $E$ and an action $+: E \times \v{E} \rightarrow E$

Consider a subset $L$ of $\mathbb{A}^2$ consisting of points satisfying

$$ -x + y - 2 = 0 $$

Where any point has the form $(x, f(x)) = (x, 2 + x)$, the line can be made into an affine space by defining $+: L \times V \rightarrow L$ (note that $V$ is a vector space) so that for any $u \in V$

$$ (x, 2 + x) + u = (x + u, 2 + x + u) $$

For example the point $(-2,0)$ added with the vector $u = [1,1]$ results in the point $(-1, 1)$ which belongs to the set $L$, note that for the example above the vector space $V$ has only vectors parallels to $u = [1,1]$

Chasles’s Identity

Given any three points $a,b,c \in E$ we know that $c = a + \mathbf{ac}$, $b = a + \mathbf{ab}$ and $c = b + \mathbf{bc}$ by the axiom 3, therefore

$$ c = b + \mathbf{bc} = (a + \mathbf{ab}) + \mathbf{bc} = a + (\mathbf{ab} + \mathbf{bc}) $$

And thus

$$ \mathbf{ab} + \mathbf{bc} = \mathbf{ac} $$

Which is known as Chasles’s identity

Affine combinations

Consider $\mathbb{R}^2$ an affine space with its origin at $(0,0)$ and basis vectors $\mathbf{b_1} = [1, 0]$ and $\mathbf{b_2} = [0,1]$, given any two points $a,b \in \mathbb{R}^2$ with coordinates $a = (a_1,a_2)$ and $b = (b_1,b_2)$ we can define the affine combination $\lambda a + \mu b$ as the point of coordinates

$$ (\lambda a_1 + \mu b_1, \lambda a_2 + \mu b_2) $$

Let $\lambda = 1, \mu = 1$, $a = (-1,1)$ and $b = (2, 2)$ then $a + b = (1, 1)$

If we change the coordinate system to have an origin at $(1,1)$ with the same basis vectors then the coordinates of the given points are $a=(-2,-2)$ and $b=(1,1)$, the linear combination is then $a + b = (-1,-1)$ which is the same as the point $(0,0)$ of the first coordinate system, therefore $a+b$ corresponds to two different points depending on the coordinate system used

A restriction is needed for affine combinations to make sense and the restriction is that the scalar add up to 1

Lemma: Given an affine space $E,v{E},+$, let $a_i, i \in I$ be a family of points in $E$ and let $\lambda_i, i \in I$ a family of scalars then any two points $a,b \in E$ the following properties hold

$$ \begin{equation} \label{lemma-1} a + \sum_{i \in I} \lambda_i \mathbf{aa_i} = b + \sum_{i \in I} \lambda_i \mathbf{ba_i} \quad \text{if $\sum_{i \in I} \lambda_i = 1$} \end{equation} $$
> > and >
$$ \begin{equation} \label{lemma-2} \sum_{i \in I} \lambda_i \mathbf{aa_i} = \sum_{i \in I} \lambda_i \mathbf{ba_i} \quad \text{if $\sum_{i \in I} \lambda_i = 0$} \end{equation} $$

To prove \eqref{lemma-1} we apply Chasles’s identity

$$ \begin{align*} a + \sum_{i \in I} \lambda_i \mathbf{aa_i} &= a + \sum_{i \in I} \lambda_i (\mathbf{ab} + \mathbf{ba_i}) \\ &= a + (\sum_{i \in I} \lambda_i) \mathbf{ab} + \sum_{i \in I} \lambda_i \mathbf{ba_i} \\ &= a + \mathbf{ab} + \sum_{i \in I} \lambda_i \mathbf{ba_i} \quad \text{since $\sum_{i \in I} \lambda_i = 1$} \\ &= b + \sum_{i \in I} \lambda_i \mathbf{ba_i} \quad \text{since $b = a + \mathbf{ab}$} \\ \end{align*} $$

For \eqref{lemma-2} we also have

$$ \begin{align*} \sum_{i \in I} \lambda_i \mathbf{aa_i} &= \sum_{i \in I} \lambda_i (\mathbf{ab} + \mathbf{ba_i}) \\ &= (\sum_{i \in I} \lambda_i) \mathbf{ab} + \sum_{i \in I} \lambda_i \mathbf{ba_i} \\ &= \sum_{i \in I} \lambda_i \mathbf{ba_i} \quad \text{since $\sum_{i \in I} \lambda_i = 0$} \\ \end{align*} $$

Formally for any family of points $a_i, i \in I$ in $E$, for any family $\lambda_i, i \in I$ of scalars such that $\sum_{i \in I} \lambda_i = 1$ the point

$$ \begin{equation} \label{affine-combination} x = a + \sum_{i \in I} \lambda_i \mathbf{aa_i} \end{equation} $$

Is independent of $a \in E$ and is called the barycenter or affine combination of the points $a_i$ with weights $\lambda_i$, and is denoted as

$$ \sum_{i \in I} \lambda_i a_i $$

Affine maps

An affine map between two affine spaces $X$ and $Y$ is a map $f: X \rightarrow Y$ that preserves affine combinations i.e.

$$ f \left (\sum_{i \in I} \lambda_i a_i \right ) = \sum_{i \in I} \lambda_i f(a_i) $$

References

  • Bærentzen, J. A., Gravesen, J., Anton François, & Aanæs, H. (2012). Guide to computational geometry processing: foundations, algorithms, and methods. London: Springer.