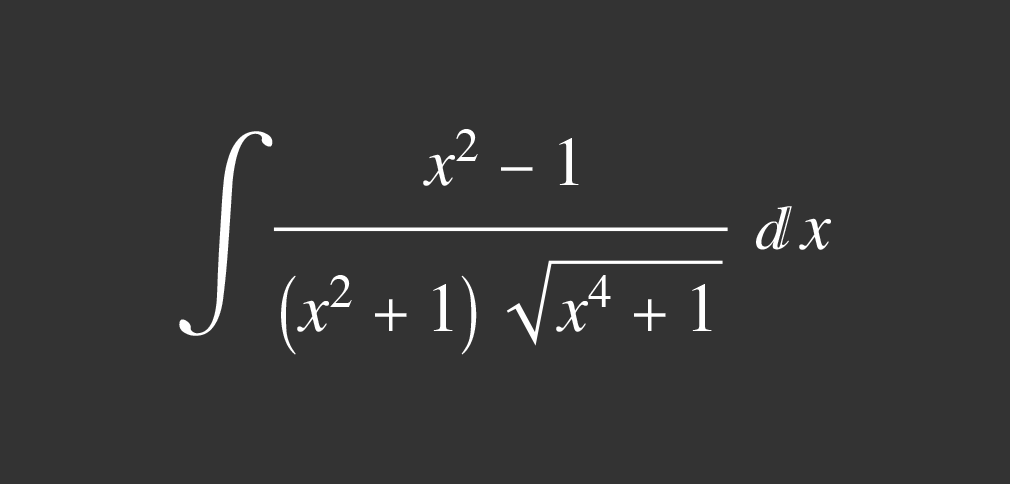Integral

We’re asked to find the derivative of the following function with respect to $x$ :

\begin{matrix} (1) & y = 3 x^{2} \end{matrix}

Performing the differentiation process:

\begin{aligned} y^{'} & = lim_{Δ x \to 0} \frac{f (x + Δ x) - f (x)}{Δ x} \\ = lim_{Δ x \to 0} \frac{3 (x + Δ x)^{2} - 3 x^{2}}{Δ x} \\ = lim_{Δ x \to 0} \frac{3 x^{2} + 6 x Δ x - Δ x^{2} - 3 x^{2}}{Δ x} \\ = lim_{Δ x \to 0} 6 x - Δ x \\ = 6 x \end{aligned}

Let’s say that we’re given the same problem in a reversed version. We’re asked to find the original function of the following derivative function:

\begin{matrix} (2) & y^{'} = 6 x \end{matrix}

Why? Because “when we formulate physical problems mathematically, the given physical information usually leads to derived functions, and the primary objective in solving the physical problems is to find the original functions” ¹.

We know that the original function corresponding to $(2)$ is $(1)$ , but is there an algorithm to find the derivative for the case above? A possible algorithm for the differentiation of the function above might be:

for each term in the function:
  - multiply the coefficient with the exponent of the independent variable
  - reduce the exponent of the independent variable by one

Reversing the algorithm above means that we’re actually trying to find the original function. A reversed version of the algorithm above might be:

for each term in the function:
  - increment the exponent of the independent variable by one
  - divide the coefficient with the exponent of the independent variable

If we apply it to $(2)$ , we get the original function:

6 x \to 6 x^{2} \to 6 / 2 x^{2} 3 x^{2}

However, we have overlooked one point. It’s also true that $(2)$ is the derived function of $y = 3 x^{2} + C$ , where $C$ is some constant. This means that a constant term that was in the original function doesn’t show up in the derived function. In view of this possibility, we must say that:

y = 3 x^{2} + C

The process of going from the derived function to the original function is called antidifferentiation or integration. The original function is called the primitive function or the indefinite integral of the given function (which is shortened to integral).

Before proving the correctness of the previous algorithm, let’s try it on similar functions. The formula for instantaneous acceleration (the instantaneous rate of change of speed with respect to time) is:

v^{'} = 32

Here, the independent variable is actually $x^{0}$ . Applying the 2-step algorithm to find the original function:

32 t^{0} \to 32 t \to 32 / 1 t 32 t

Same as above, since the original function might have had a constant:

v = 32 t + C

Straight Line Motion in One Direction

Galileo obtained a basic physical principle: if one neglects air resistance, all objects near the Earth’s surface fall to Earth with the same acceleration, which is constant (a downward acceleration). The constant value is equal to:

32 feet/s

Find how long it takes for an object dropped from 400 feet above the Earth’s surface to reach the surface.

The instantaneous acceleration, as seen above, is:

a = v^{'} = 32

Applying the 2-step algorithm:

v = 32 t + C

If the object is dropped, it leaves with zero speed (when $t = 0$ , $v = 0$ ). Substituting these values in the formula above to find the value of $C$ :

0 = 32 \cdot 0 + C C = 0

Therefore, the correct formula for speed is:

\begin{matrix} (3) & v = s^{'} = 32 t \end{matrix}

Applying a new process of antidifferentiation to $(3)$ :

s = 16 t^{2} + C

If we agree to measure distance from the point the object is dropped, then the initial distance when $t = 0$ is also zero. $C$ will also have a value of zero. Hence, the correct formula for distance is:

s = 16 t^{2}

To answer the original equation, we must find out the value of $t$ given that $s = 400$ :

t = \pm \sqrt{\frac{s}{16}} = \pm \sqrt{\frac{400}{16}} = \pm \sqrt{25} = \pm 5

For the physical problem, only the positive solution is valid. With the same knowledge, we can also tackle problems where the object is thrown instead of dropped.

Find how long it takes for an object thrown downward with a velocity of 100 ft/s from a height of 1000 feet to reach the Earth’s surface.

Starting with the formula of instantaneous acceleration:

a = 32

Applying the 2-step algorithm:

v = 32 t + C

The object is thrown downwards instead of dropped, which means that when $t = 0,; v = 100$ :

100 = 32 \cdot 0 + C C = 100

Hence, the correct formula for speed is:

v = 32 t + 100

Applying a new process of antidifferentiation:

s = 16 t^{2} + 100 t + C

If we agree to measure the distance from the point where the object is thrown, then $C = 0$ :

s = 16 t^{2} + 100 t

It’s convenient to measure distance from the Earth’s surface and not from any arbitrary distance like the examples above. However, this means that the upward direction is positive. Then the acceleration of gravity must be negative, i.e., $- 32; f t / s e c^{2}$ , so that the distance traveled by reason of this acceleration is recorded as downward.

v^{'} = - 32 f t / s e c^{2}

Then by antidifferentiation:

\begin{matrix} (4) & v = - 32 t + C \end{matrix}

If an object is thrown upward, it must have an initial upward velocity. Let’s say that an object located on the Earth’s surface is thrown upward with an initial velocity equal to $128; f t / s$ . Substituting these values in $(4)$ (when $t = 0,; v = 128$ ):

128 = - 32 \cdot 0 + C C = 128

so that:

\begin{matrix} (5) & v = - 32 t + 128 \end{matrix}

Applying a new process of antidifferentiation to find the distance traveled upward at any time $t$ :

s = - 16 t^{2} + 128 t + C

Because we have agreed to measure distance from the surface, the value of $C$ is zero because when $t = 0$ , the object is still on the ground:

\begin{matrix} (6) & s = - 16 t^{2} + 128 t \end{matrix}

One question of interest is the maximum height attained by an object whose motion is represented by $(6)$ . This problem could be answered if we knew at what $t$ the object attains maximum height. However, we can use $(5)$ to obtain the time since we know that the instant the object attains maximum height, the velocity will be zero (the object will rise until its velocity is zero and then fall). Substituting zero as the speed in $(5)$ :

0 = - 32 t + 128 t = \frac{128}{32} = 4

Now that we know the time at which the object attains the maximum height, let’s replace it in $(6)$ :

\begin{aligned} s & = - 16 (4)^{2} + 128 \cdot 4 \\ = - 256 + 512 \\ = 256 feet \end{aligned}

We can generalize the solutions above for objects thrown on any planet. We can represent the acceleration with the symbol $g$ , so the acceleration due to this gravity felt from the ground is:

\begin{matrix} (7) & a = - g \end{matrix}

By antidifferentiation:

v = - g t + C

Since it’s a generalization, we don’t know the initial velocity (the value of $C$ is some constant). Let’s represent the initial velocity of the object with the symbol $v_{0}$ . Hence, the formula for the velocity is:

\begin{matrix} (8) & v = v_{0} - g t \end{matrix}

Applying a new process of antidifferentiation to find the distance of the object from the ground:

s = v_{0} t - \frac{g t^{2}}{2} + C

For this case, we also don’t know the initial distance from the ground the object is when $t = 0$ . Let’s represent the initial distance from the ground with the symbol $s_{0}$ :

\begin{matrix} (9) & s = s_{0} + v_{0} t - \frac{g t^{2}}{2} \end{matrix}

Definite Integral

Area as the Limit of the Sum

Let’s say we want to compute the area of the graph below $f (x)$ and the $x$ -axis bounded by the vertical lines $x = a = 1$ and $x = b = 2$ :

f (x) = x^{2}

An approximation to the area can be found by taking the maximum y-value in $(a, b)$ , called $m_{1}$ , and multiplying it by $(b - a)$ , which will be expressed as $Δ (x)$ . Then the first approximation is $m_{1} Δ x$ :

S_{1} = m_{1} Δ x

We can obtain a better approximation if we divide the interval $(a, b)$ into two equal parts, each denoted by $Δ x$ , multiplied by the maximum y-value in each part, and then form the sum:

S_{2} = m_{1} Δ x + m_{2} Δ x

Dividing the interval $(a, b)$ into $n$ equal parts, each denoted as $Δ x$ , and choosing $n$ maximum y-values for each part, we form the sum:

S_{n} = m_{1} Δ x + m_{2} Δ x + \dots + m_{n} Δ x

The quantity $n$ can increase without a limit. To each $n$ , there’s a corresponding sum. Now the quantity:

lim_{n \to \infty} S_{n}

seems to give the exact area under the curve bounded by $a$ and $b$ . Therefore:

lim_{n \to \infty} S_{n} = A

There is another notation for this limit which keeps the bounds that determine the area. If $y = f (x)$ , then we write for the limit:

\int_{a}^{b} f (x) d x

The elongated S denotes integration. The symbols $a$ and $b$ are the left and right ends of the domain whose area is being calculated, and $f (x) d x$ is a reminder that we took rectangles of height $y_{i}$ and width $Δ x_{i}$ .

Evaluation of Definite Integrals

Another way to find the area is as follows. Previously, we found an approximation of the area as ( $Δ x \cdot max (f (x))$ for all $x \in [a, b]$ ). Similarly, we can take the lower bound instead ( $Δ x \cdot min (f (x))$ for all $x \in [a, b]$ ). Let’s assume that somehow we have found the area below the curve bounded by $[a, x_{0}]$ . Moving $x_{0}$ to the right will generate an increment in the area. This change in the area can be expressed as:

Δ A = \bar{y} \cdot Δ x

\frac{Δ A}{Δ x} = \bar{y}

The value of $\bar{y}$ is some value between $f (x_{0})$ and $f (x_{0} + Δ x)$ . To obtain the instantaneous rate of change in the area with respect to $x$ , we must find the limit of $Δ A / Δ x$ as $Δ x$ approaches zero. Also, as $Δ x$ approaches zero, the value of $\bar{y}$ also approaches $f (x_{0})$ . Therefore:

\frac{d A}{d x} = y_{0} = f (x_{0})

Because this is true for any value of $x$ in the interval $[a, b]$ :

\frac{d A}{d x} = y = f (x)

To find the value of $A (x)$ , we apply antidifferentiation:

A = \int f (x) d x

As an example, let’s apply the above to the function $f (x) = x^{2}$ :

\begin{matrix} (10) & A = \int x^{2} d x = \frac{x^{3}}{3} + C \end{matrix}

When $x = a = 1$ , we know that the area is zero. Then:

\begin{aligned} 0 & = \frac{1^{3}}{3} + C \\ C & = - \frac{1}{3} \end{aligned}

Then:

A = \frac{x^{3}}{3} - \frac{1}{3}

is the function which expresses the area from $a$ to any position $x$ . To find the area bounded by $[a, b]$ , we substitute $x = b = 2$ and get:

A = \frac{2^{3}}{3} - \frac{1}{3} = \frac{7}{3}

We can obtain the same result if we take the expression $(10)$ , substituting 2 for $x$ , 1 for $x$ , and then subtracting the second result from the first:

\frac{2^{3}}{3} + C - (\frac{1}{3} + C) = \frac{7}{3}

The constant of integration is eliminated in the process. This process is actually called the fundamental theorem of calculus:

\int_{a}^{b} f (x) d x = F (b) - F (a)

Where $F (x)$ is the antiderivative of $f (x)$ .

Additional Properties of the Definite Integral

\int_{a}^{b} f (x) d x = - \int_{b}^{a} f (x) d x

\int_{a}^{b} f (x) d x = \int_{a}^{x_{0}} f (x) d x + \int_{x_{0}}^{b} f (x) d x

\int_{a}^{b} u d x \pm \int_{a}^{b} v d x = \int_{a}^{b} (u \pm v) d x

\frac{d}{d x} \int_{a}^{x} u d u = f (x)

Numerical Methods for Evaluating Definite Integrals

Trapezoid Rule

Let’s imagine that we have a curve for which it’s impossible to find the antiderivative, and thus the area below the curve. Instead of calculating it, we can approximate its value by using trapezoids instead of rectangles, as we’ve done before. We also know that approximating the area below the curve using the $min (f (x))$ value found in the interval $[a, b]$ multiplied by $b - a$ (denoted as $Δ x$ ) gives a lower bound of the area below the curve:

\underset{―}{S_{n}} = y_{0} Δ x + y_{1} Δ x + \dots y_{n - 1} Δ x

Another approximation was using the $max (f (x))$ value found in the interval $[a, b]$ multiplied by $b - a$ (denoted as $Δ x$ ), which gives the upper bound of the area below the curve:

\overset{―}{S_{n}} = y_{1} Δ x + y_{2} Δ x + \dots y_{n} Δ x

Calculating the average of these sums will definitely give an approximate result:

S_{n} = \frac{1}{2} (y_{0} + y_{1}) Δ x + \frac{1}{2} (y_{1} + y_{2}) Δ x + \dots + \frac{1}{2} (y_{n - 1} + y_{n}) Δ x

Each of these terms is the area of a trapezoid of height $Δ x$ and bases $y_{i}$ , $y_{i + 1}$ .

Rewriting the equation above:

\int_{a}^{b} f (x) d x \approx Δ x \cdot (\frac{1}{2} y_{0} + y_{1} + y_{2} + \dots + y_{n - 1} + \frac{1}{2} y_{n})

[Simpson’s Rule][simpson]

Simpson’s rule approximates the value of a definite integral by using quadratic polynomials of the form:

\begin{matrix} (11) & y = a x^{2} + b x + c \end{matrix}

which pass through three points belonging to the curve, which are $(- h, y_{0})$ , $(0, y_{1})$ , and $(h, y_{2})$ .

The area below the curve bounded by $[- h, h]$ is:

\begin{aligned} A & = \int_{- h}^{h} (a x^{2} + b x + c) d x \\ = \frac{a x^{3}}{3} + \frac{b x^{2}}{2} + c x |_{- h}^{h} \\ = \frac{2 a h^{3}}{3} + 2 c h \\ = \frac{h}{3} (2 a h^{2} + 6 c) \end{aligned}

Since the points $(- h, y_{0})$ , $(0, y_{1})$ , and $(h, y_{2})$ are on the curve, they satisfy $(11)$ :

\begin{aligned} y_{0} & = a h^{2} - b h + c \\ y_{1} & = c \\ y_{2} & = a h^{2} + b h + c \end{aligned}

The quantity:

y_{0} + 4 y_{1} + y_{2} = (a h^{2} - b h + c) + 4 c + (a h^{2} + b h + c) = 2 a h^{2} + 6 c

is equal to a part of the area under the quadratic polynomial found above. Therefore:

A = \frac{h}{3} (y_{0} + 4 y_{1} + y_{2})

To find the area bounded by $[a, b]$ , we have to take an even number $n$ of subintervals of equal length:

h = \frac{b - a}{n}

$n$ subintervals are defined with $n + 1$ points, which are:

x_{0} = a, x_{1} = a + h, x_{2} = a + 2 h, \dots, x_{n} = a + n h = b

We can estimate the value of the integral by adding the areas computed for each unique contiguous pair of subintervals:

\begin{aligned} \int_{a}^{b} f (x) d x & \approx \frac{h}{3} (y_{0} + 4 y_{1} + y_{2}) + \frac{h}{3} (y_{2} + 4 y_{3} + y_{4}) + \dots + \frac{h}{3} (y_{n - 2} + 4 y_{n - 1} + y_{n}) \\ \approx \frac{h}{3} (y_{0} + 4 y_{1} + 2 y_{2} + 4 y_{3} + 2 y_{4} + \dots + 4 y_{n - 1} + y_{n}) \end{aligned}

Physical Applications of the Definite Integral

The Calculation of Work

When a force applied to an object causes a displacement, it’s said that work was done upon the object. This quantity, expressed with the symbol $W$ , is the product:

W = F s

As an example, let’s calculate the work done by the force of gravity. Choosing the direction from the center of the Earth upward as the positive direction, we can use Newton’s law for gravitation. This law states that any two objects attract each other, and this force is given quantitatively by:

F = \frac{G m M}{r^{2}}

$G$ is a constant, $m$ and $M$ are the masses of the two objects, and $r$ is the distance between the objects (idealized as point particles).

Since this force of gravity actually pulls objects towards the center of the Earth, and we chose the direction from the center of the Earth upward as positive, this quantity must be negative:

\begin{matrix} (12) & F = - \frac{G m M}{r^{2}} \end{matrix}

To calculate the work done by gravity, we cannot multiply the force of gravity by the displacement because the force actually varies from point to point along the path. Suppose the object is at some distance $r$ from the center of the Earth and gravity pulls the object downward a small distance $Δ r$ . Then the work done by gravity is:

Δ W = F Δ r

By division:

\frac{Δ W}{Δ r} = F

We now determine the limit of $\frac{Δ W}{Δ r}$ as $Δ r$ approaches 0, which is the rate of change of work with respect to the displacement over the path:

\frac{d W}{d r} = lim_{Δ r \to 0} \frac{Δ W}{Δ r} = F

Replacing $(12)$ :

\frac{d W}{d r} = - \frac{G m M}{r^{2}}

To find $W$ , we apply an antidifferentiation process:

W = \int - \frac{G m M}{r^{2}} = \frac{G m M}{r} + C

Assuming that initially, when the object was at $r = r_{1}$ , there was no force being applied to it, therefore $W = 0$ and $C = - G m M / r_{1}$ , and:

W = \frac{G m M}{r} - \frac{G m M}{r_{1}}

Excerpt From: Morris Kline. “Calculus: An Intuitive and Physical Approach (Second Edition).” [simpson]: http://pages.pacificcoast.net/~cazelais/187/simpson.pdf ↩︎