2D Rotation
A 2D rotation has only one parameter, $\theta$. When the basis vectors $\unit{i} = [1, 0]$ and $\unit{j} = [0, 1]$ are rotated by an angle $\theta$:
$$
\mathbf{p} = \cos{\theta} \unit{i} + \sin{\theta} \unit{j} \\
\mathbf{q} = -\sin{\theta} \unit{i} + \cos{\theta} \unit{j}
$$
Which builds the rotation matrix:
$$
\mathbf{R}(\theta) = \begin{bmatrix}
\textbf{p} \\
\textbf{q}
\end{bmatrix} = \begin{bmatrix}
\cos{\theta} & \sin{\theta} \\
-\sin{\theta} & \cos{\theta}
\end{bmatrix}
$$
When a vector $\mathbf{v}$ is transformed by this matrix, we know that the vector will be a linear combination of the basis, which are $\mathbf{p}$ and $\mathbf{q}$:
$$
\begin{align*}
\mathbf{v'} = \mathbf{vR}(\theta) &= v_x \mathbf{p} + v_y \mathbf{q} \\
&= v_x \begin{bmatrix}\cos{\theta} & \sin{\theta}\end{bmatrix} + v_y \begin{bmatrix}-\sin{\theta} & \cos{\theta}\end{bmatrix} \\
&= \begin{bmatrix}
v_x \cos{\theta} - v_y \sin{\theta} \\
v_x \sin{\theta} + v_y \cos{\theta}
\end{bmatrix}^T
\end{align*}
$$
Using a matrix to encode this operation:
$$
\begin{align*}
\mathbf{v'} = \mathbf{vR}(\theta) &= \begin{bmatrix}v_x & v_y\end{bmatrix} \begin{bmatrix}
\cos{\theta} & \sin{\theta} \\
-\sin{\theta} & \cos{\theta}
\end{bmatrix} \\
&= \begin{bmatrix}
v_x \cos{\theta} - v_y \sin{\theta} \\
v_x \sin{\theta} + v_y \cos{\theta}
\end{bmatrix}^T
\end{align*}
$$
See also
complex numbers
.
3D Rotation
About Cardinal Axes
$$
\mathbf{R_x}(\alpha) = \begin{bmatrix}
1 & 0 & 0 \\
0 & \cos{\alpha} & -\sin{\alpha} \\
0 & \sin{\alpha} & \cos{\alpha}
\end{bmatrix}
$$
$$
\mathbf{R_y}(\beta) = \begin{bmatrix}
\cos{\beta} & 0 & \sin{\beta} \\
0 & 1 & 0 \\
-\sin{\beta} & 0 & \cos{\beta}
\end{bmatrix}
$$
$$
\mathbf{R_z}(\gamma) = \begin{bmatrix}
\cos{\gamma} & -\sin{\gamma} & 0 \\
\sin{\gamma} & \cos{\gamma} & 0 \\
0 & 0 & 1
\end{bmatrix}
$$
See also:
About an Arbitrary Axis
Given an axis $\unit{n}$ and an amount of rotation around it $\theta$, our goal is to find a rotation matrix that rotates about $\unit{n}$ by the angle $\theta$:
$$
\mathbf{v'} = \mathbf{R}(\unit{n}, \theta)\mathbf{v}
$$
The basic idea is to solve this problem in a plane perpendicular to $\unit{n}$, which becomes a 2D problem.
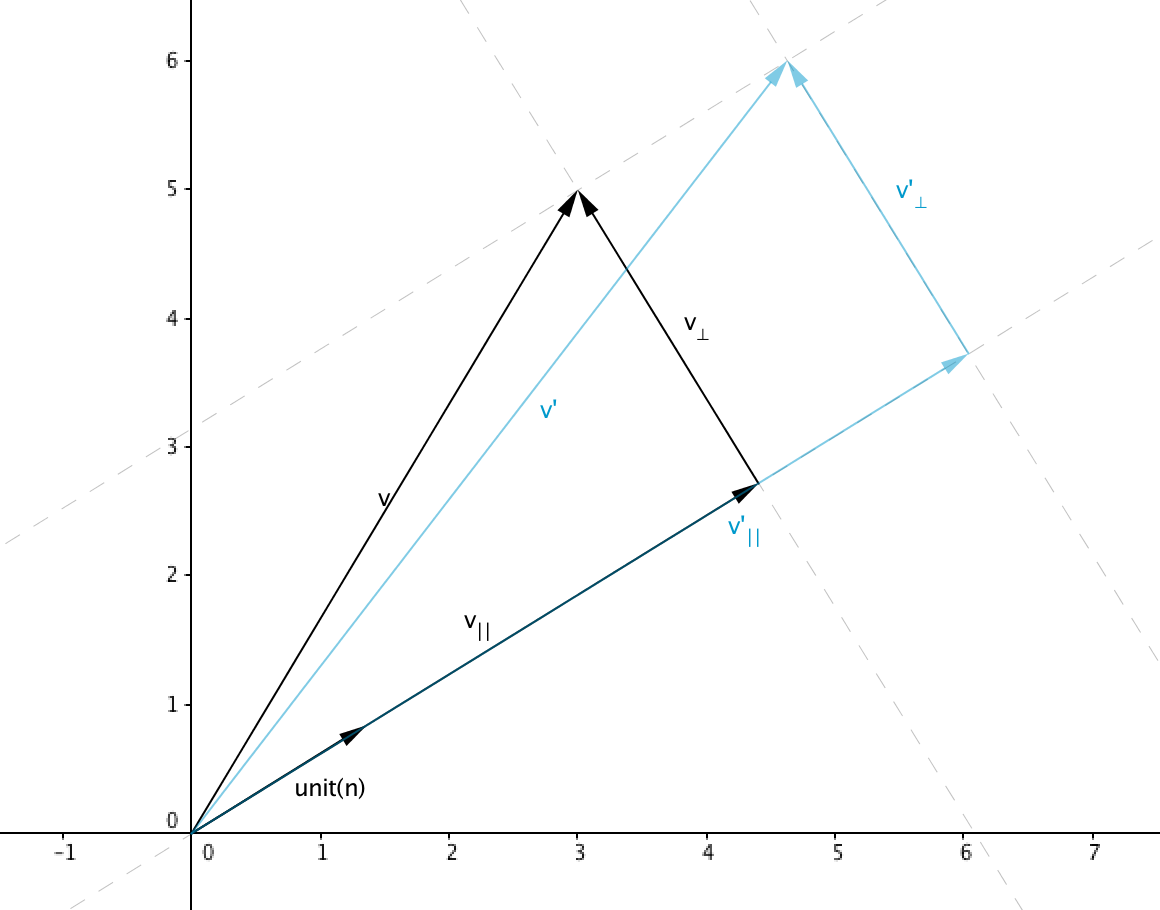
Separate $\mathbf{v}$ into two vectors: a vector parallel to $\unit{v}$ called $\mathbf{v_{\parallel}}$ and a vector perpendicular to $\unit{v}$ called $\mathbf{v_{\perp}}$ such that $\mathbf{v_{\parallel}} + \mathbf{v_{\perp}} = \mathbf{v}$:
$$
\begin{align*}
\mathbf{v_{\parallel}} &= (\mathbf{v} \cdot \unit{n}) \unit{n} \\
\mathbf{v_{\perp}} &= \mathbf{v} - \mathbf{v_{\parallel}}
\end{align*}
$$
After the rotation, it’s obvious that the $\mathbf{v_{\parallel}}$ component will be the same, and only the vector $\mathbf{v_{\perp}}$ will be rotated.
A plane can be defined with two vectors that lie on it. Since we have $\mathbf{v_{\perp}}$ and we also know the normal of the plane (which is $\unit{n}$), any vector perpendicular to both vectors will also lie in the plane. We can use the cross product to find this vector:
$$
\mbold{w} = \unit{n} \times \mbold{v_{\perp}}
$$
The length of $\mbold{w}$ is:
$$
\begin{align*}
\left \| \mbold{w} \right \| &= \left \| \unit{n} \right \| \left \| \mbold{v_{\perp}}\right \| \sin{\deg{90}} \\
&= \left \| \mbold{v_{\perp}}\right \|
\end{align*}
$$
Which means that $\mbold{w}$ has the same length as $\mbold{v_{\perp}}$. Note that even though they have the same length, they don’t necessarily have unit length.
$\mbold{w}$ and $\mbold{v_{\perp}}$ now form a 2D coordinate space where the $x$-axis is $\mbold{v_{\perp}}$ and the $y$-axis is $\mbold{w}$.
Let $\mbold{v_{\perp}’}$ be a vector that is the result of rotating $\mbold{v_{\perp}}$ by an angle $\theta$. We can find the projection of it onto the $x$-axis and the $y$-axis as follows:
$$
\begin{align*}
\mbold{v_{\perp,x}'} &= (\magnitude{ \mbold{v_{\perp}} } \cos{\theta}) \unit{v_{\perp}} = \cos{\theta} \mbold{v_{\perp}}\\
\mbold{v_{\perp,y}'} &= (\magnitude{ \mbold{v_{\perp}} } \sin{\theta}) \unit{w} = \sin{\theta} \mbold{w}
\end{align*}
$$
- Expressing $\mbold{v_{\perp}’}$ as a linear combination of the basis:
$$
\mbold{v_{\perp}'} = \cos{\theta} \mbold{v_{\perp}} + \sin{\theta} \mbold{w}
$$
Reconstructing the solution from the observations above:
$$
\begin{align*}
\mbold{v_{\parallel}} &= (\mbold{v} \cdot \unit{n}) \unit{n} \\
\mbold{v_{\perp}} &= \mbold{v} - \mbold{v_{\parallel}} \\
&= \mbold{v} - (\mbold{v} \cdot \unit{n}) \unit{n} \\
\mbold{w} &= \unit{n} \times \mbold{v_{\perp}} \\
&= \unit{n} \times (\mbold{v} - \mbold{v_{\parallel}}) \\
&= \unit{n} \times \mbold{v} - \unit{n} \times \mbold{v_{\parallel}} \\
&= \unit{n} \times \mbold{v}
\end{align*}
$$
Finally:
$$
\begin{align}
\mbold{v'} &= \mbold{v_{\perp}'} + \mbold{v_{\parallel}'} \nonumber \\
&= \cos{\theta} \mbold{v_{\perp}} + \sin{\theta} \mbold{w} + (\mbold{v} \cdot \unit{n}) \unit{n} \nonumber \\
&= \cos{\theta} (\mbold{v - (\mbold{v} \cdot \unit{n}) \unit{n}}) + \sin{\theta} (\unit{n} \times \mbold{v}) + (\mbold{v} \cdot \unit{n}) \unit{n} \nonumber \\
&= \cos{\theta} \mbold{v} - \cost (\mathbf{v} \cdot \unit{n}) \unit{n} + \sin{\theta} (\unit{n} \times \mbold{v}) + (\mbold{v} \cdot \unit{n}) \unit{n} \nonumber \\
&= \cos{\theta} \mbold{v} + \sin{\theta} (\unit{n} \times \mbold{v}) + (1 - \cost)(\mathbf{v} \cdot \unit{n}) \unit{n} \label{3d-rotation}
\end{align}
$$
Now we can compute what the basis vectors are after the transformation above (by using each of the basis vectors as $\mbold{v}$ on \eqref{3d-rotation}) to construct a rotation matrix:
$$
\begin{align*}
\mbold{p} &= \begin{bmatrix}1 \\ 0 \\ 0\end{bmatrix} \quad \quad \quad \quad \mbold{p'} = \begin{bmatrix}
n_x^2(1 - \cost) + \cost \\
n_xn_y(1 - \cost) + n_z \sint \\
n_xn_z(1 - \cost) - n_z \sint
\end{bmatrix}\\
\\
\mbold{q} &= \begin{bmatrix}0 \\ 1 \\ 0\end{bmatrix} \quad \quad \quad \quad \mbold{q'} = \begin{bmatrix}
n_yn_x(1 - \cost) - n_z \sint \\
n_y^2(1 - \cost) + \cost \\
n_yn_z(1 - \cost) + n_x \sint
\end{bmatrix}\\
\\
\mbold{r} &= \begin{bmatrix}0 \\ 0 \\ 1\end{bmatrix} \quad \quad \quad \quad \mbold{r'} = \begin{bmatrix}
n_zn_x(1 - \cost) + n_y \sint \\
n_zn_y(1 - \cost) - n_x \sint \\
n_z^2(1 - \cost) + \cost
\end{bmatrix}\\
\end{align*}
$$
Constructing the matrix from these vectors:
$$
\mathbf{R}(\unit{n}, \theta) =
\begin{bmatrix}
\mbold{p'} & \mbold{q'} & \mbold{r'}
\end{bmatrix}
$$
3D Rotations Using Quaternions
A complex rotor is a unit norm complex number that rotates another complex number by the angle $\theta$ and has the form:
$$
e^{i\theta} = \cos{\theta} + i \sin{\theta}
$$
Hamilton had hoped that a unit-norm quaternion $q$ could be used to rotate a vector, which is stored as a pure quaternion $p$. The unit norm quaternion is given by:
$$
\begin{align}
q &= [s, \lambda \unit{n}] \quad s,\lambda \in \mathbb{R}, \unit{n} \in \mathbb{R}^3 \label{unit-norm-quaternion} \\
\left | \unit{n} \right | &= 1 \nonumber \\
s^2 + \lambda^2 &= 1 \nonumber
\end{align}
$$
$$
p = [0, \mbold{v}] \quad \mbold{v} \in \mathbb{R}^3
$$
Let’s compute the product $p’ = qp$:
$$
\begin{align}
p' &= qp \nonumber \\
&= [s, \lambda \unit{n}][0, \mathbf{v}] \nonumber \\
&= [-\lambda \unit{n} \cdot \mathbf{v}, s \mathbf{v} + \lambda \unit{n} \times \mathbf{v}] \label{p-prime}
\end{align}
$$
Special Case
What if $\unit{n}$ is perpendicular to $\mathbf{v}$? Then the scalar quantity of \eqref{p-prime} is zero, and we are left with the pure quaternion:
$$
\begin{equation} \label{p-prime-perpendicular}
p' = [0, s \mathbf{v} + \lambda \unit{n} \times \mathbf{v}] \quad\quad \text{given that $\unit{n}$ is perpendicular to $\mathbf{v}$}
\end{equation}
$$
Let’s analyze the vector part of $\eqref{p-prime-perpendicular}$ (which is now a 3D entity because it’s a pure quaternion). Since $\unit{n}$ is perpendicular to $\mathbf{v}$, then the vector $\unit{n} \times \mathbf{v}$ will have a norm equal to $\magnitude{ \unit{n} \times \mathbf{v} } = \magnitude{ \unit{n} } \magnitude { \mathbf{v} } \sin{\deg{90}}$. Also, since $\unit{n}$ is a unit vector, then $\magnitude{\unit{n} \times \mathbf{v}} = \magnitude{\mathbf{v}}$, which means that we have two orthogonal vectors with the same length.
To rotate the vector $\mathbf{v}$ about $\unit{n}$, let’s transform $\mathbf{v}$ to the 2D space whose basis vectors are $\mathbf{v}$ and $\unit{n} \times \mathbf{v}$ and perform the rotation there, which is trivially $[\cos{\theta}, \sin{\theta}]$. Therefore, all we have to do in \eqref{p-prime-perpendicular} is make the scalar quantities multiplying each vector equal to the projection of the rotated vector over the basis:
$$
p' = [0, \cos{\theta} \mathbf{v} + \sin{\theta} \unit{n} \times \mathbf{v}]
$$
Which makes the quaternion $\mathbf{q}$ have the form:
$$
\begin{align}
q &= [\cos{\theta}, \sin{\theta}\unit{n}] \label{perp-rotor}
\end{align}
$$
And it acts as a rotor only when $\unit{n}$ is perpendicular to $\mathbf{v}$.
Important notes/facts about orthogonal quaternions:
- If $q$ is a rotor about the unit vector $\unit{n}$ by an angle $\theta$ whose vector term is perpendicular to the pure quaternion $p$:
- $qp$ and $pq^{-1}$ rotate $p$ by an angle $\theta$ about $\unit{n}$.
- $pq$ and $q^{-1}p$ rotate $p$ by an angle $-\theta$ about $\unit{n}$.
- Each of these products leaves $p’$ unscaled (because $q$ is a unit norm quaternion).
General Case
Let’s use \eqref{unit-norm-quaternion} as the starting point. Note that this time its vector part is not necessarily perpendicular to the pure quaternion $p$. The product $qp$ yields:
$$
\begin{align*}
qp &= [s, \lambda \unit{n}][0, \mathbf{v}] \\
&= [-\lambda \unit{n} \cdot \mathbf{v}, s \mathbf{v} + \lambda \unit{n} \times \mathbf{v}]
\end{align*}
$$
Note that the term $-\lambda \unit{n} \cdot \mathbf{v}$ does not vanish since for the general case, $\unit{n}$ and $\mathbf{v}$ are no longer perpendicular. What’s more important is that the product $qp$ is no longer a pure quaternion. Multiplying a vector by a non-orthogonal quaternion has converted some of the vector information into the quaternion’s scalar component.
What happens if we post-multiply $qp$ by $q^{-1}$? Could it reverse the operation? (Note that since $q$ is a norm quaternion, $q^{-1} = q^*$.)
$$
qpq^{-1} = [-\lambda \unit{n} \cdot \mathbf{v}, s \mathbf{v} + \lambda \unit{n} \times \mathbf{v}][s, -\lambda \unit{n}]
$$
Let’s first check if doing this multiplication makes the scalar component vanish:
$$
\begin{align*}
qpq^{-1} &= [-\lambda s \unit{n} \cdot \mathbf{v} - (s \mathbf{v} + \lambda \unit{n} \times \mathbf{v}) \cdot (-\lambda \unit{n}), \ldots] \\
&= [-\lambda s \unit{n} \cdot \mathbf{v} + (s \mathbf{v}) \cdot (\lambda \unit{n}) + (\lambda \unit{n} \times \mathbf{v}) \cdot (\lambda \unit{n}), \ldots] \\
&= [-\lambda s \unit{n} \cdot \mathbf{v} + (s \mathbf{v}) \cdot (\lambda \unit{n}) + 0, \ldots] \quad \text {since $\unit{n}$ is perpendicular to $\unit{n} \times \mathbf{v}$ } \\
&= [-\lambda s \unit{n} \cdot \mathbf{v} + \lambda s \mathbf{v} \cdot \unit{n}), \ldots] \\
&= [0, \ldots]
\end{align*}
$$
Indeed, it magically made the scalar component vanish! Now let’s look at the vector component of $qpq^{-1}$:
$$
\begin{align*}
qpq^{-1} &= [0, s (s \mathbf{v} + \lambda \unit{n} \times \mathbf{v}) + (-\lambda \unit{n} \cdot \mathbf{v})(-\lambda \unit{n}) + (s \mathbf{v} + \lambda \unit{n} \times \mathbf{v}) \times (-\lambda \unit{n})] \\
&= [0, s^2 \mathbf{v} + s \lambda (\unit{n} \times \mathbf{v}) + \lambda^2 (\unit{n} \cdot \mathbf{v})\unit{n} - s \lambda (\mathbf{v} \times \unit{n}) - \lambda^2 (\unit{n} \times \mathbf{v} \times \unit{n})]
\end{align*}
$$
Let’s
expand the cross product
:
$$
(\unit{n} \times \mathbf{v}) \times \unit{n} = (\unit{n} \cdot \unit{n}) \mathbf{v} - (\mathbf{v} \cdot \unit{n}) \unit{n} = \mathbf{v} - (\mathbf{v} \cdot \unit{n}) \unit{n}
$$
Therefore:
$$
\begin{align*}
qpq^{-1} &= [0, s^2 \mathbf{v} + s \lambda (\unit{n} \times \mathbf{v}) + \lambda^2 (\unit{n} \cdot \mathbf{v})\unit{n} - s \lambda (\mathbf{v} \times \unit{n}) - \lambda^2 (\mathbf{v} - (\mathbf{v} \cdot \unit{n}) \unit{n})] \\
&= [0, s^2 \mathbf{v} + s \lambda (\unit{n} \times \mathbf{v}) + \lambda^2 (\unit{n} \cdot \mathbf{v})\unit{n} - s \lambda (\mathbf{v} \times \unit{n}) - \lambda^2 \mathbf{v} + \lambda^2 (\mathbf{v} \cdot \unit{n}) \unit{n})] \\
&= [0, s^2 \mathbf{v} + 2 s \lambda (\unit{n} \times \mathbf{v}) + \lambda^2 (\unit{n} \cdot \mathbf{v})\unit{n} - \lambda^2 \mathbf{v} + \lambda^2 (\mathbf{v} \cdot \unit{n}) \unit{n})] \\
&= [0, (s^2 - \lambda^2) \mathbf{v} + 2 s \lambda (\unit{n} \times \mathbf{v}) + 2 \lambda^2 (\mathbf{v} \cdot \unit{n}) \unit{n}] \\
\end{align*}
$$
Let’s make $s = \cos{\theta}$ and $\lambda = \sin{\theta}$, just like in \eqref{perp-rotor} (it worked as a rotor when it was orthogonal to $p$; it might work with the general case too):
$$
qpq^{-1} = [0, (\cos^2{\theta} - \sin^2{\theta}) \mathbf{v} + 2 \cos{\theta} \sin{\theta} (\unit{n} \times \mathbf{v}) + 2 \sin^2{\theta} (\mathbf{v} \cdot \unit{n}) \unit{n}]
$$
Which involves double-angle terms. Replacing these terms with
double-angle identities
:
$$
qpq^{-1} = [0, \cos{2\theta} \mathbf{v} + \sin{2\theta} (\unit{n} \times \mathbf{v}) + (1 - \cos{2\theta}) (\mathbf{v} \cdot \unit{n}) \unit{n}]
$$
The product created a pure quaternion equal to $\mathbf{v}$ rotated by an angle of $2\theta$. If we want to rotate $\mathbf{v}$ by an angle of $\theta$, we must build a half-angle $\theta$ quaternion $q$ (note above that $q$ was equal to \eqref{perp-rotor}):
$$
\begin{equation} \label{rotor}
q = [\cos{\frac{1}{2}\theta}, \sin{\frac{1}{2}\theta}\unit{n}]
\end{equation}
$$
Using \eqref{rotor}, the product is:
$$
qpq^{-1} = [0, \cos{\theta} \mathbf{v} + \sin{\theta} (\unit{n} \times \mathbf{v}) + (1 - \cos{\theta}) (\mathbf{v} \cdot \unit{n}) \unit{n}]
$$
Note that the vector part of $qpq^{-1}$ is identical to \eqref{3d-rotation}.
Quaternion Difference and Dot Product
Let $a$ and $b$ be two unit norm quaternions (rotors that have the same form as \eqref{rotor}). The quaternion to rotate from $a$ to $b$ is given by $da = b$ and is known as quaternion difference. Finding the value of $d$ given that we know $a$ and $b$:
$$
\begin{align*}
da &= b \\
d(aa^*) &= ba^* \quad \quad \text{since $a$ is a unit norm quaternion, its inverse is equal to its conjugate} \\
d &= ba^*
\end{align*}
$$
Expanding the product:
$$
\begin{align*}
d &= [s_b, \mathbf{b}][s_a, -\mathbf{a}] \\
&= [s_bs_a + \mathbf{b} \cdot \mathbf{a}, -s_b\mathbf{a} + s_a\mathbf{b} - \mathbf{b} \times \mathbf{a}]
\end{align*}
$$
Note that the scalar part of this quaternion is equal to the inner product (a generalization of the dot product to abstract vector spaces) between two quaternions:
$$
d = [\left \langle a, b \right \rangle, -s_b\mathbf{a} + s_a\mathbf{b} - \mathbf{b} \times \mathbf{a}]
$$
Remembering that a rotor is given by \eqref{rotor}, we can relate the inner product between rotor quaternions with the scalar quantity of \eqref{rotor} and interpret it geometrically, just like the dot product between two vectors in 3D/2D space, but this time noticing that the dot product gives the cosine of half the angle between the quaternions:
$$
a \cdot b = \cos{\frac{\theta}{2}}
$$
This means that the angle between $a$ and $b$ is equal to:
$$
\theta = 2 \arccos{(a \cdot b)}
$$
Or using the
half-angle formulas
:
$$
\begin{align*}
\cos^2{\frac{\theta}{2}} &= \frac{1}{2}(1 + \cos{\theta}) \\
(a \cdot b)^2 &= \frac{1}{2}(1 + \cos{\theta}) \\
\cos{\theta} &= 2 (a \cdot b)^2 - 1 \\
\theta &= \arccos(2(a \cdot b)^2 - 1)
\end{align*}
$$
The second formula works for all cases, as noted
here
(the first one doesn’t work when $a \cdot b < 0$).
