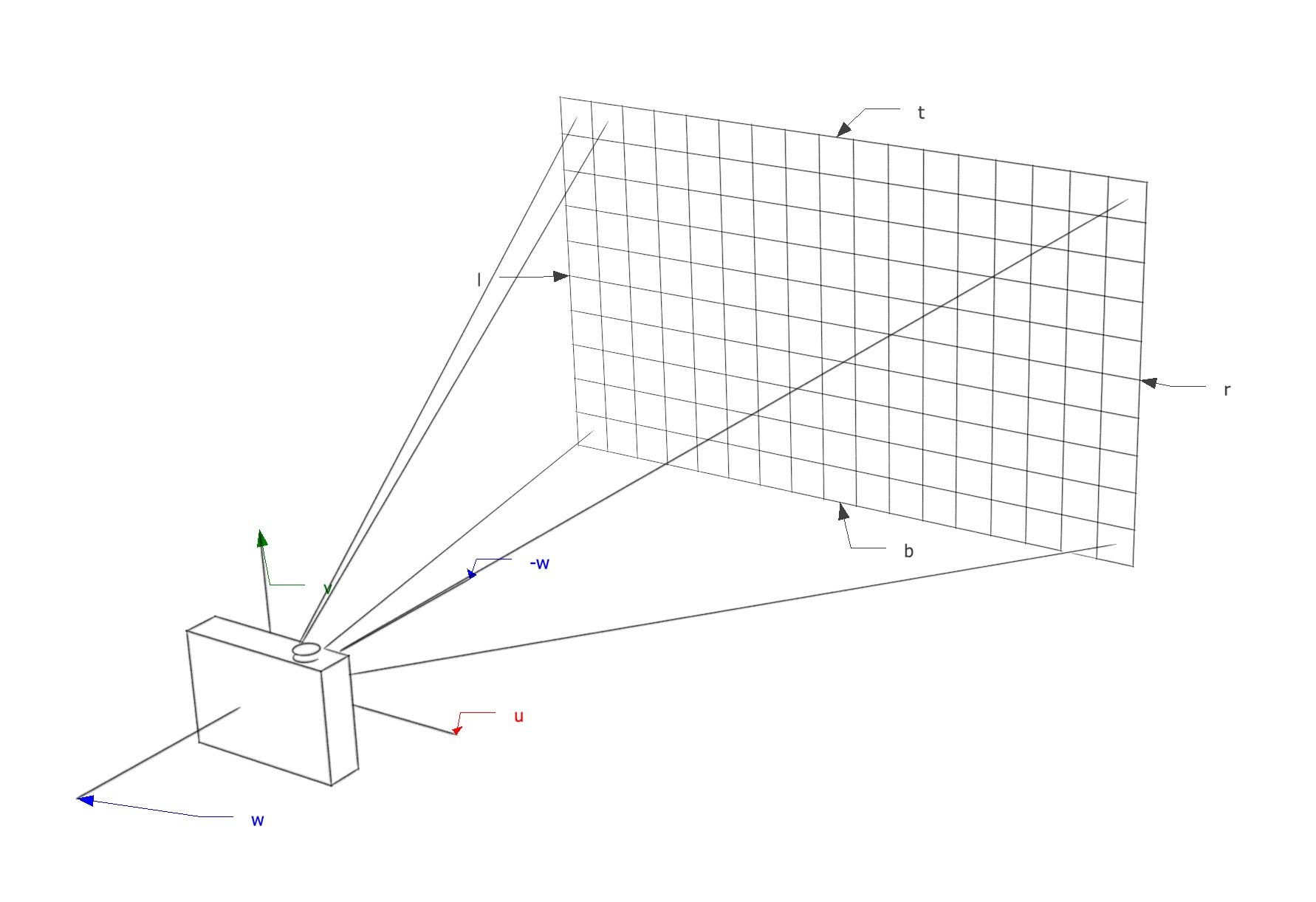
As seen in projective geometry , the perspective phenomenon is where an object appears to be smaller the further away it is from the point of view.

We can again use some concepts of projective geometry to understand perspective projection, particularly the fact that any object in our 3D world is represented in the 4D projective hyperplane by the homogeneous coordinate (x,y,z,1). Now, any finite point with wot=1 can be projected to the 4D hyperplane w=1 by dividing each coordinate by w, i.e., (xw,yw,zw). A key observation in the values of w is that the higher the value of w, the smaller the object will be when it gets projected to the w=1 hyperplane.

Perspective is implemented in 3D by using a transformation matrix that changes the value of w based on how far the object is (the z-coordinate).

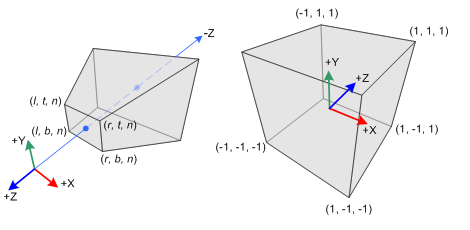
Now, let’s imagine that we want to project the points that exist in our world to the plane z=d.

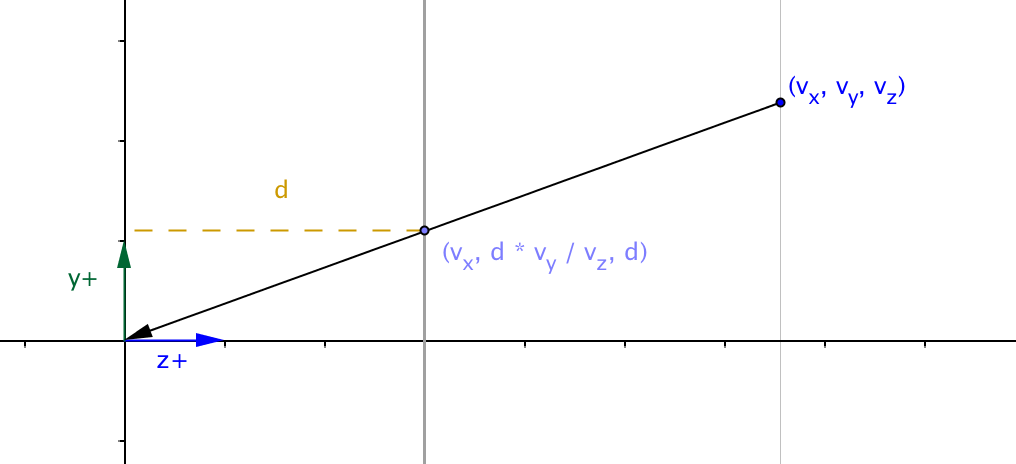
Perspective Projection Y

Perspective Projection Y

By similar images, we can see that the projected value of the y-coordinate is:

vy′d=vyvz⇒vy′=dvyvz

The projected value of the x-coordinate can be computed in a similar way:

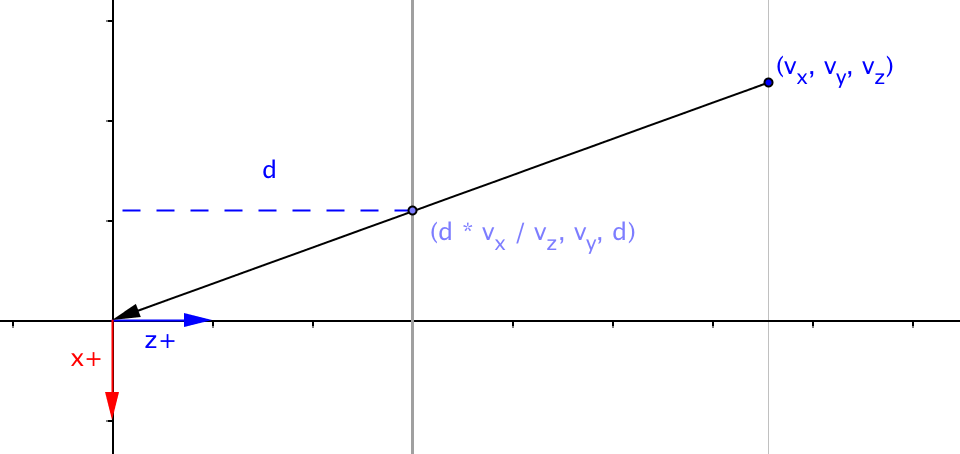
Perspective Projection X

Perspective Projection X

vx′d=vxvz⇒vx′=dvxvz

The projected value of the z-coordinate is the same for all the points:

vz′=d

Summarizing:

v′=[dvxvzdvyvzd]T

Manipulating the last equation so that it has a common denominator:

v′=[dvxvzdvyvzdvzvz]T=[vxvyvz]Tvzd

The point above expressed in 4D homogeneous coordinates is:

v′=[vxvyvzvzd]T

Finally, the transformation matrix that transforms v to v′ is:

v′=[100001000010001d0][vxvyvz1]=[vxvyvzvzd]