Minimum Spanning Tree

If a connected graph $G$ of order $n$ has no cycles, then, of course, $G$ is a tree. Let’s suppose that $G$ contains cycles. Let $e_{1}$ be an edge lying on a cycle of $G$ . We know that since $e_{1}$ is part of a cycle, it’s not a bridge, which means that $G - e_{1}$ is connected. If $G - e_{1}$ contains cycles, then let $e_{2}$ be an edge lying on a cycle of $G - e_{1}$ . $e_{2}$ is not a bridge, and therefore $G - e_{1} - e_{2}$ is still connected. Eventually, we arrive at the set $X = e_{1}, e_{2}, \dots, e_{k}$ of edges such that $G - X$ doesn’t contain cycles (i.e., it’s a tree) and has the same vertex set as $G$ ( $V (G) = V (G - X)$ ).

Let $T = G - X$ be a tree with the same vertex set as $G$ .

$T$ is a spanning subgraph of $G$ . Since $T$ is also a tree, it’s called a spanning tree of $G$ .

Minimum spanning tree

The purpose of finding a minimum spanning tree (MST) is to identify the subset of edges of a given connected, undirected graph that forms a tree, connecting all the vertices and having the minimum possible total edge weight.

Let $G$ be a connected weighted graph where the weight of an edge $e \in E (G)$ is denoted by $w (e)$ . For each subgraph $H$ of $G$ , the weight of the subgraph $W$ is the sum of the weights of its edges.

w (H) = \sum_{e \in E (H)} w (e)

We are looking for a spanning tree of $G$ whose weight is the minimum among all spanning trees of $G$ . Such a spanning tree is called a minimum spanning tree (shortened as MST)

\begin{aligned} G & = (V, E) \\ V & = {0, 1, 2, 3, 4} \\ E & = {{0, 1}, {0, 2}, {0, 3}, {0, 4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {3, 4}} \\ w (e) & = {1, 4, 4, 5, 3, 7, 5, 6, 2} \end{aligned}

The MST is unique if the weights of all the edges are different.
The maximum spanning tree is the tree whose weight is maximum among all spanning trees. It can be computed using the algorithm below by using the edges with the maximum weight instead of the ones with the minimum weight.

Kruskal’s algorithm

For a connected weighted graph $G$ , a spanning tree is constructed as follows:

For the first edge, $e_{1}$ , we select any edge of $G$ with minimum weight.
For the second edge, $e_{2}$ , we select any remaining edge of $G$ with minimum weight.
For the third edge, $e_{3}$ , we select any remaining edge of $G$ with minimum weight that does not produce a cycle with the previously selected edges.
We continue in this manner until a spanning tree is produced.

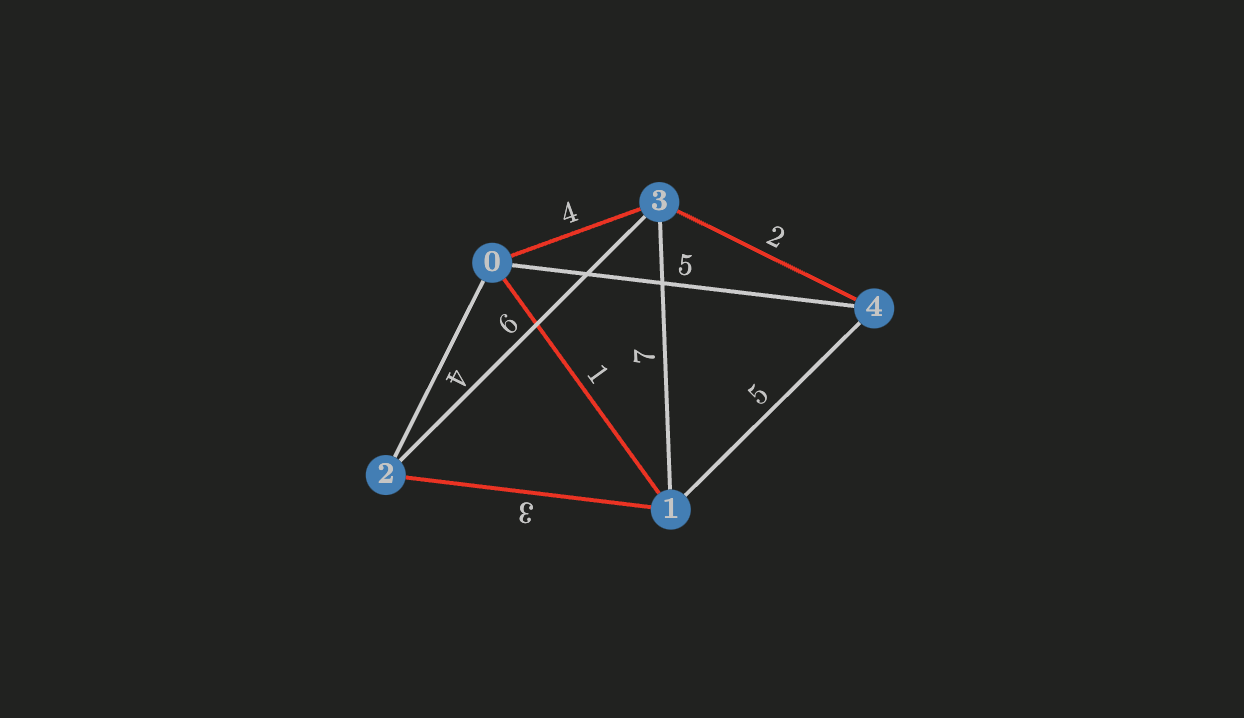
Let’s apply it to the weighted graph above. Sorting the edges in nondecreasing order, we have:

w (e) = {1, 2, 3, 4, 4, 5, 5, 6, 7}

Some properties of the edges:

The edge with the minimum cost is $e_{1} = v_{0} v_{1}$ with $w (e_{1}) = 1$ . $e_{1}$ is part of the MST.
The edge with the minimum cost is now $e_{9} = v_{3} v_{4}$ with $w (e_{9}) = 2$ . $e_{9}$ is part of the MST.
The next edge is $e_{5} = v_{1} v_{2}$ with $w (e_{5}) = 3$ . Since it does not form a cycle with the previously selected edges, it’s part of the MST.
The next edge is $e_{2} = v_{0} v_{2}$ with $w (e_{2}) = 4$ . This one forms a cycle with the path $v_{0}, v_{1}, v_{2}$ , so it’s not part of the MST.
The next edge is $e_{3} = v_{0} v_{3}$ with $w (e_{3}) = 4$ . Since it does not form a cycle with the previously selected edges, it’s part of the MST.
There’s no need to do more iterations since the set is already a spanning tree.

struct edge {
  int u, v, weight;
  edge(int _u, int _v, int _w) {
    u = _u; v = _v; weight = _w;
  }
  // custom sort
  bool operator<(const edge &other) const {
    return weight < other.weight;
  }
};

vector<int> tree, size;

void initialize_sets(int n) {
  tree.resize(n);
  size.resize(n);
  for (int i = 0; i < n; i += 1) {
    tree[i] = i;
    size[i] = 1;
  }
}

int find_set(int element) {
  if (element != tree[element]) {
    tree[element] = find_set(tree[element]);
  }
  return tree[element];
}

void set_union(int x, int y) {
  int rx, ry;
  rx = find_set(x);
  ry = find_set(y);
  if (rx == ry) {
    return;
  }
  if (rx > ry) {
    size[rx] += size[ry];
    tree[ry] = rx;
  } else {
    size[ry] += size[rx];
    tree[rx] = ry;
  }
}

/**
 * An implementation of Kruskal's algorithm which computes
 * the minimum spanning tree of a graph `G`
 *
 * Time complexity: O(m log m)
 * Space complexity: O(m)
 *
 * @param {vector<vector<pair<int, int> > >} g The adjacency list representation
 * of a graph `G`, each entry `g_{ij}` holds a pair which represents an edge
 * (vertex, weight) which tells that there's an edge from `i` to `vertex`
 * with weight `weight`
 * @return {int} The weight of the MST
 */
int kruskal(vector<vector<pair<int, int> > > &g) {
  int n = g.size();

  vector<edge> edges;
  for (int i = 0; i < n; i += 1) {
    for (int j = 0; j < g[i].size(); j += 1) {
      int v = g[i][j].first;
      int weight = g[i][j].second;
      edges.push_back(edge(i, v, weight));
    }
  }

  initialize_sets(n);

  sort(edges.begin(), edges.end());

  int total = 0;
  for (int i = 0; i < edges.size(); i += 1) {
    int u = find_set(edges[i].u);
    int v = find_set(edges[i].v);
    if (u != v) {
      set_union(u, v);
      total += edges[i].weight;
    }
  }

  return total;
}

Prim’s algorithm

For a connected weighted graph $G$ , a spanning tree is constructed as follows:

For an arbitrary vertex $u$ , an edge of minimum weight $e_{1}$ incident to $u$ is chosen as the first edge of the MST.
For subsequent edges $e_{2}, e_{3}, \dots, e_{n - 1}$ , we select an edge of minimum weight among those edges having exactly one of its vertices incident with an edge already selected.

Prim in dense graphs

Let’s say we’re given the following problem:

Given $n$ points in a plane, find the skeleton of minimum weight that connects them all.

This problem can be modeled as a graph of order $n$ where each vertex is connected to every other vertex by an edge with a weight equal to the Euclidean distance between the vertices; therefore, $m \approx n^{2}$ .

Implementation strategies:

We need a data structure that keeps track of a single edge per vertex (space: $O (n)$ ) and is able to find the one with the minimum weight (doing $O (n)$ queries). Since $m \approx n^{2}$ , we visit each vertex, finding an edge with minimum cost (each query will take $O (n)$ for an overall $O (n^{2})$ time complexity).
After an arbitrary vertex $u$ has been chosen, all the vertices incident to $u$ will update their minimum edge weight.

/**
 * An implementation of Prim's algorithm which computes
 * the minimum spanning tree of a dense graph `G`
 *
 * Time complexity: O(n^2)
 * Space complexity: O(n)
 *
 * @param {vector<vector<int> >} g The adjacency matrix of `G`, each entry `a_{ij}`
 * holds the weight of the edge connecting vertex `i` and vertex `j`, if this number
 * is <= 0 then `i` and `j` are not adjacent
 * @return {int} The weight of the MST
 */
int prim(vector<vector<int> > &g) {
  int n = g.size();
  int INF = 1e9;
  int total = 0;

  vector<bool> visited(n, false);
  // holds the weight of the edge of minimum weight incident
  // to the vertex `i`
  vector<int> min_weight_edge(n, INF);
  // (optional) holds the index of a vertex adjacent to the
  // vertex `i` in the MST, note that the size of the MST is
  // n - 1 so the first vertex won't store the mentioned index
  vector<int> neighbor_selected(n, -1);

  // pick the first node as the "arbitrary" node
  min_weight_edge[0] = 0;

  for (int i = 0; i < n; i += 1) {
    int v = -1;
    for (int j = 0; j < n; j += 1) {
      // find the vertices which haven't been visited yet
      // among them find a vertex with the minimum edge weight
      if (!visited[j] && (v == -1 ||
          min_weight_edge[j] < min_weight_edge[v])) {
        v = j;
      }
    }

    visited[v] = true;
    total += min_weight_edge[v];

    // update the minimum edge weight of all the vertices
    // adjacent to `v`
    for (int to = 0; to < n; to += 1) {
      if (g[v][to] > 0 &&
          g[v][to] < min_weight_edge[to]) {
        min_weight_edge[to] = g[v][to];
        // update the candidate neighbor of the vertex `to` to
        // be `v` since it's connected with an edge
        // of minimum weight among all the adjacent vertices to `to`
        neighbor_selected[to] = v;
      }
    }
  }

  return total;
}

Prim in sparse graphs

Implementation strategies:

We need a data structure that keeps track of a single edge per vertex (space: $O (n)$ ) and is able to find the one with the minimum weight (doing $O (n)$ queries). Since $m \approx n$ , we analyze each edge, finding the one with the minimum weight $O (n)$ times. We can use a red-black tree (each operation takes $O (\log n)$ for an overall $O (m; \log; n)$ time complexity).
After an arbitrary vertex $u$ has been chosen, all the vertices incident to $u$ will update their minimum edge weight.
The red-black tree will hold at most $n - 1$ entries (one entry per vertex). In each iteration, a vertex will be removed from the red-black tree.
There will be exactly $n$ iterations if the graph is connected.

/**
 * C++11
 *
 * An implementation of Prim's algorithm which computes
 * the minimum spanning tree of a sparse graph `G` of order `n` and size `m`
 *
 * Time complexity: O(m log n)
 * Space complexity: O(n)
 *
 * @param {vector<vector<pair<int, int> > >} g The adjacency list representation
 * of a graph `G`, each entry `g_{ij}` holds a pair which represents an edge
 * (vertex, weight) which tells that there's an edge from `i` to `vertex`
 * with weight `weight`
 * @return {int} The weight of the MST or a negative number if the graph
 * wasn't connected
 */
int prim(vector<vector<pair<int, int> > > &g) {
  int n = g.size();
  int total = 0;

  vector<bool> visited(n, false);
  // holds the weight of the edge of minimum weight incident
  // to the vertex `i`
  vector<int> min_cost(n, INF);
  // (optional) holds the index of a vertex adjacent to the
  // vertex `i` in the MST, note that the size of the MST is
  // n - 1 so the first vertex won't store the mentioned index
  vector<int> neighbor(n, -1);

  // the first node is the "arbitrary" node for the sake of the implementation
  min_cost[0] = 0;

  // (min weight, vertex)
  set<pair<int, int> > q;
  q.insert({0, 0});

  while (!q.empty()) {
    int v = q.begin()->second;

    // the vertex `v` belongs to the MST and is adjacent
    // to the vertex `neighbor[v]` with and edge
    // of weight `weight`
    total += q.begin()->first;

    q.erase(q.begin());

    visited[v] = true;

    for (int i = 0; i < g[v].size(); i += 1) {
      pair<int, int> &next = g[v][i];

      // note that in the graph the first element is the neighbor vertex
      // but in the set the first element is the edge weight
      int to = next.first;
      int weight = next.second;

      if (!visited[to] && weight < min_cost[to]) {
        q.erase({ min_cost[to], to });
        min_cost[to] = weight;
        neighbor[to] = v;
        q.insert({ min_cost[to], to });
      }
    }
  }
  // check that every vertex has a min cost edge associated
  for (int i = 0; i < n; i += 1) {
    if (min_cost[i] == INF) {
      return -1;
    }
  }
  return total;
}

Number of spanning trees in a graph

Let $G$ be a graph with $V (G) = v_{1}, v_{2}, \dots, v_{n}$ . Let $A = [a_{i j}]$ be the adjacency matrix of $G$ , and let $C = [c_{i j}]$ be an $n \times n$ matrix where:

c_{i j} = {\begin{cases} d e g v_{i} & if i = j \\ - a_{i j} & if i \neq j \end{cases}

Then the number of spanning trees of $G$ is the value of any cofactor of $C$ .

The matrix of cofactors is an $n \times n$ matrix $C = [c_{i j}]$ where:

c_{i j} = (- 1)^{i + j} \cdot d e t (M_{i j})

$d e t (M_{i j})$ indicates the determinant of the $(n - 1) \times (n - 1)$ submatrix of $M$ obtained by removing the $i$ -th row and the $j$ -th column.

/**
 * Given a square matrix M of size (n x n) this method
 * computes the a matrix of size (n - 1) x (n - 1) by eliminating
 * the elements belonging to the `row` row of M and the `col`
 * column of M
 *
 * @param {vector<vector<int> > } m The square matrix
 * @param {int} row The row to be ignored
 * @param {int} col The column to be ignored
 * @return {vector<vector<int> >} the value of the determinant
 */
vector<vector<int> > minor(vector<vector<int> > m, int row, int col) {
  int n = m.size();
  vector<vector<int> > t(n - 1, vector<int>(n - 1));

  int trow = 0;
  for (int i = 0; i < n; i += 1) {
    if (i == row) {
      continue;
    }
    int tcol = 0;
    for (int j = 0; j < n; j += 1) {
      if (j == col) {
        continue;
      }
      t[trow][tcol] = m[i][j];
      tcol += 1;
    }
    trow += 1;
  }
  return t;
}

/**
 * Computes the determinant of an square matrix
 *
 * @param {vector<vector<int> > } m The square matrix
 * @return {int} the value of the determinant
 */
int determinant(vector<vector<int> > m) {
  int n = m.size();

  if (n == 1) {
    return m[0][0];
  }
  if (n == 2) {
    return m[0][0] * m[1][1] - m[1][0] * m[0][1];
  }

  int result = 0;
  for (int col = 0; col < n; col += 1) {
    vector<vector<int> > t = minor(m, 0, col);
    result += m[0][col] * pow(-1, col) * determinant(t);
  }
  return result;
}

/**
 * Computes the number of spanning trees in an undirected graph `G`
 *
 * @param <vector<vector<int> > > g The adjacency matrix of `G`
 * @return {int} The number of spanning trees
 */
int number_of_spanning_trees(vector<vector<int> > &g) {
  int n = g.size();
  vector<vector<int> > t = g;
  for (int i = 0; i < n; i += 1) {
    // -a_{ij} for elements that are not in the main diagonal
    int degree = 0;
    for (int j = 0; j < n; j += 1) {
      if (i != j) {
        t[i][j] *= -1;
        if (t[i][j]) {
          degree += 1;
        }
      }
    }

    // deg v_i for t[i][i]
    t[i][i] = degree;
  }

  // compute the (0,0) cofactor
  // c_{0, 0} = (-1)^{0 + 0} * determinant((0, 0) minor)
  //          = determinant((0, 0) minor)
  return determinant(minor(t, 0, 0));
}

Number of spanning trees in a complete graph $K_{n}$

Computing the number of spanning trees of a graph $G = K_{n}$ , where $V (G) = v_{1}, v_{2}, \dots, v_{n}$ , is the same as computing the number of distinct trees with the vertex set $v_{1}, v_{2}, \dots, v_{n}$ . The formula is called the Cayley Tree Formula.

The number of spanning trees of order $n$ with a specific vertex set is $n^{n - 2}$ .

Minimum spanning tree

Kruskal’s algorithm

Prim’s algorithm

Prim in dense graphs

Prim in sparse graphs

Number of spanning trees in a graph

Number of spanning trees in a complete graph Kn

Hamiltonian Graphs

Eulerian Graph and Eulerian Trails

Single Source Shortest Path (SSSP) in a graph

Number of spanning trees in a complete graph $K_{n}$