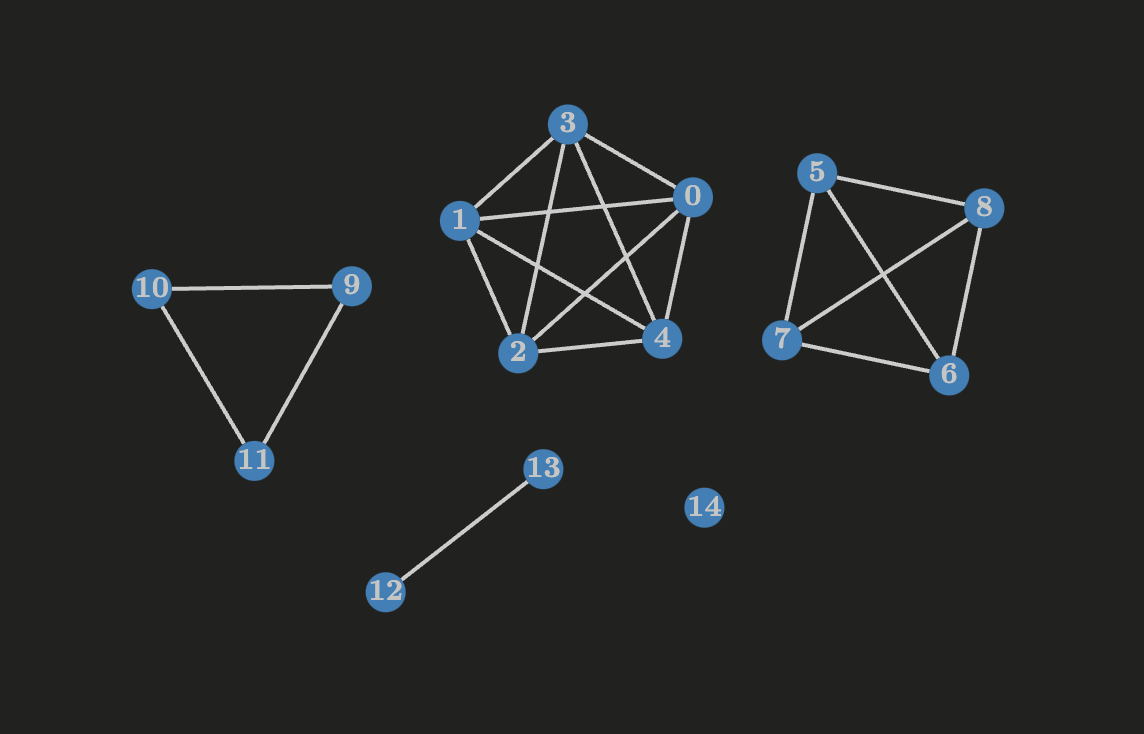
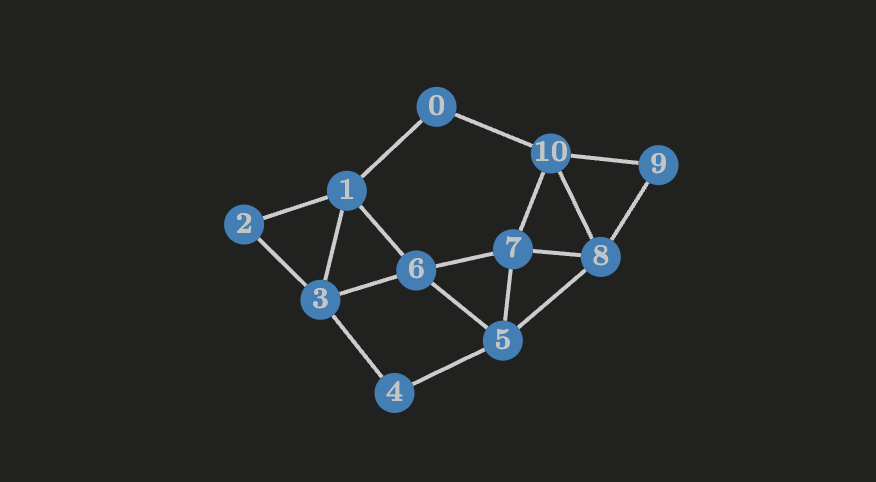
Breadth First Search (BFS)

Given a graph $G$ and a distinguished source vertex $s$, BFS explores the edges of $G$ to discover the vertices adjacent to $s$. As a consequence, it also computes the distance of the path from $s$ to each reachable vertex.

vector<int> dist;
vector<int> parent;

/**
 * Traverses a graph `G` of order `n` and size `m` by breadth
 *
 * Time complexity: O(n + m)
 * Space complexity: O(n)
 *
 * @param {vector<vector<int> >} g The adjacency list representation
 * of a graph
 * @param {int} source The source vertex
 */
void bfs(vector<vector<int> > &g, int source) {
  int n = g.size();
  dist.assign(n, -1);
  parent.assign(n, -1);

  queue<int> remaining;
  dist[source] = 0;
  remaining.push(source);

  while (!remaining.empty()) {
    int current = remaining.front();
    remaining.pop();

    for (int i = 0; i < g[current].size(); i += 1) {
      int next = g[current][i];
      if (dist[next] == -1) {
        dist[next] = dist[current] + 1;
        parent[next] = current;
        remaining.push(next);
      }
    }
  }
}

Depth First Search (DFS)

Given a graph $G$ and a distinguished source vertex $s$, DFS explores the edges incident to $s$ and explores as far as possible along each branch before backtracking. To prevent infinite loops caused by visiting a vertex multiple times, an additional state is used in each vertex, which denotes if the vertex was visited before.

Whenever a vertex $v$ is discovered by some vertex $u$, we say that $u$ is a predecessor of $v$. Also, since every vertex can only have one predecessor (a vertex can only be visited once) during the traversal, the algorithm forms a tree called the DFS tree.

During the process of creating the DFS tree, the algorithm can also define timestamps on each vertex (an integer denoting the time an action happened).

• $v_{in}$ recorded when $v$ is first discovered.
• $v_{out}$ recorded when the search finishes exploring $v s adjacent vertices.

Properties

• The number of descendants of any vertex $v$ is equal to $\frac{v_f-v_d-1}{2}$.
• For any two vertices $u$ and $v$, exactly one of the following holds:
• If the intervals $[u_{in},u_{out}]$ and $[v_{in},v_{out}]$ are disjoint, then neither $u$ is a descendant of $v$ nor is $v$ a descendant of $u$ in the DFS tree.
• If the interval $[u_{in},u_{out}]$ is contained in $[v_{in},v_{out}]$, then $u$ is a descendant of $v$.
• If the interval $[v_{in},v_{out}]$ is contained in $[u_{in},u_{out}]$, then $v$ is a descendant of $u$.

Classification of edges

We can define four edge types produced by a DFS on $G$:

1. Tree edges: An edge $uv$ is a tree edge if $v$ was first discovered by $u$.
2. Back edges: An edge $uv$ is a back edge if it connects $u$ with an ancestor of $v$.
3. Forward edges: An edge $uv$ is a forward edge if it connects $u$ with a descendant of $v$ (a non-tree edge).
4. Cross edges: All other edges, e.g., an edge between branches in the DFS tree.

We can identify these edges with an additional state stored in the vertices of the graph during the DFS tree process. The additional state will be $v_{color}$ and can have three possible values:

• $v_{color}=WHITE$ if a vertex hasn’t been explored yet.
• $v_{color}=GRAY$ when a vertex is first discovered.
• $v_{color}=BLACK$ when a vertex has finished exploring its adjacent vertices.

During the analysis of an edge, we can look at the color of the adjacent vertex to determine the type of edge. Given the edge $uv$, there are three possible outcomes:

• If $v_{color}=WHITE$, then $uv$ is a tree edge.
• If $v_{color}=GRAY$, then $uv$ is a back edge.
• If $v_{color}=BLACK$, then $uv$ is a forward/cross edge.

Another way to determine the type of edge is by analyzing the states $u_{in}$ ($u_{out}$ is undefined when all the edges $uv$ are being analyzed) and $v_{in},v_{out}$ of the incident vertices to the edge. Given an edge $uv$:

• If $v_{in}$ is not defined, then $uv$ is a tree edge.
• If $v_{in}$ is defined and $v_{out}$ is not defined, then $uv$ is a back edge.
• If $v_{in}$ is defined, $v_{out}$ is defined, and $u_{in}<v_{in}$, then $uv$ is a forward edge.
• If $v_{in}$ is defined, $v_{out}$ is defined, and $u_{in}>v_{in}$, then $uv$ is a cross edge.

Additional properties of the edges

• If $G$ is an undirected graph, then every edge of $G$ is either a tree edge or a back edge during the exploration of the DFS tree.
• A directed graph $G$ is acyclic if it contains no back edges.

int time_spent = 0;

// the adjacency list of `G`
vector<vector<int> > g;
// the explored state of a vertex `i`
vector<bool> visited;
// the predecesor of a vertex `i` in the dfs tree
vector<bool> predecessor;
// the time a vertex `i` was discovered first
vector<int> time_in;
// the time a vertex `i` spent exploring each reachable non-visited vertices
vector<int> time_out;

/**
 * Traverses a graph `G` of order `n` and size `m` by depth,
 * it's assumed that `time_in`, `time_out`, `visited`, `predecessor`
 * are initialized correctly with a size equal to `n`
 *
 * Time complexity: O(n + m)
 * Space complexity: O(n)
 *
 * @param {int} v The current vertex being analyzed
 */
void dfs(int v) {
  visited[v] = true;
  time_in[v] = ++time_spent;

  for (int i = 0; i < g[v].size(); i += 1) {
    int next = g[v][i];

    // edge analysis
    if (!time_in[next]) {
      // edge (v, next) is a tree edge
    } else if (!time_out[next]) {
      // edge (v, next) is a back edge
    } else if (time_in[v] < time_in[next]) {
      // edge (v, next) is a forward edge
    } else {
      // edge (v, next) is a forward edge
    }

    // traversal to adjacent vertices
    if (!visited[next]) {
      predecessor[next] = v;
      dfs(next);
    }
  }

  time_out[v] = ++time_spent;
}