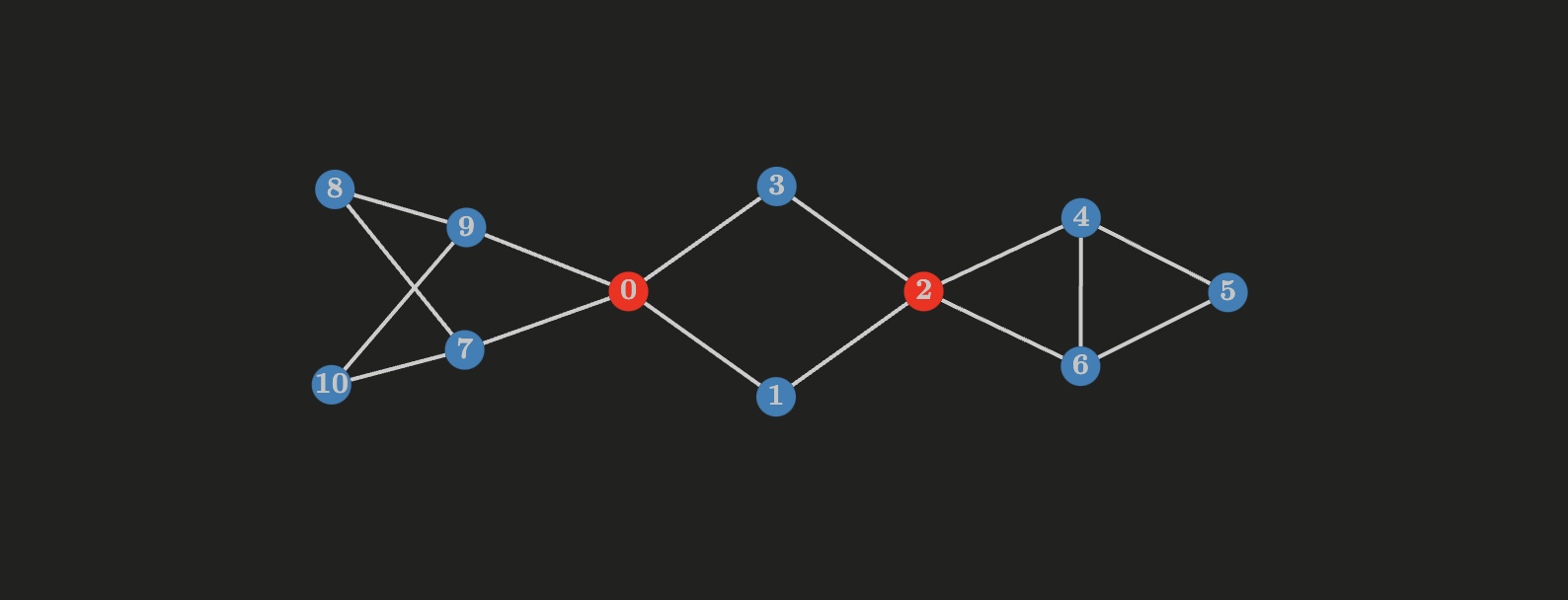
All the facts/properties below are considered for an undirected, connected graph $G$.

• If $v$ is a vertex incident with a bridge in a graph $G$, then $v$ is a cut-vertex if $deg(v)\ge 2$ (if $deg(v)=1$, then $v$ is an end-vertex of $G$, so $G-v$ is still connected).
• Given that the order of $G$ is $\ge 3$, if it contains a bridge, then it also contains a cut-vertex.
• If $v$ is a cut-vertex of $G$, and $u$ and $w$ are vertices in different components formed by $G-v$, then $v$ is part of every $u-w$ path in $G$.
• Let $u\in V(G)$. If $v$ is a vertex that is farthest from $u$, then $v$ is not a cut-vertex.

Let $G$ be an undirected graph. By analyzing the properties of the DFS tree, we can determine if a vertex is an articulation point given the following facts:

• A leaf vertex is not a cut-vertex.
• Let $u$ and $v$ be two vertices of the DFS tree such that $u$ is an ancestor of $v$.
  • If $u$ and $v$ are not adjacent and there’s a back edge $vw$ to some vertex $w$ such that $w$ is a predecessor of $u$, then none of the vertices in the $u-v$ path are cut-vertices.
  • If $u$ and $v$ are not adjacent and there’s a back edge from $v$ to some vertex in the $u-v$ path, then $u$ is a cut-vertex.
• Let $u$ be the root node of the DFS tree. It’s a cut-vertex if, during the exploration of its successor vertices, it’s found that it has more than one child, i.e., the root has more than one branch in the DFS tree.

int time_spent;

// the adjacency list representation of `G`
vector<vector<int> > g;
// the time a vertex `i` was discovered first
vector<int> time_in;
// stores the discovery time of the lowest predecessor that vertex `i`'s
// succesor vertices can reach **through a back edge**, initially
// the lowest predecessor is set to the vertex itself
vector<int> back;
// the articulation points found during the dfs
vector<int> cut_vertex;

void dfs(int v, int parent) {
  // the lowest back edge discovery time of `v` is
  // set to the discovery time of `v` initally
  back[v] = time_in[v] = ++time_spent;

  // count the number of children for the `root` vertex
  int children = 0;
  int is_cut_vertex = false;

  for (int i = 0; i < g[v].size(); i += 1) {
    int next = g[v][i];

    if (next == parent) {
      continue;
    }

    if (time_in[next] == -1) {
      dfs(next, v);
      /// if there's a back edge between a descendant of `next` and
      // a predecessor of `v` then `next` will have a lower reachable
      // vertex than `v` through a back edge, in this case the vertex `v` is not
      // a cut-vertex (the special case of the root node is handled below)
      if (back[next] >= time_in[v] && parent != -1) {
        is_cut_vertex = true;
      }
      // propagation of the back edge to a vertex with the lowest discovery time
      back[v] = min(back[v], back[next]);
      ++children;
    } else {
      // * back edge *
      // update index of the vertex incident with this back edge to
      // be the one with the lowest discovery time
      // it's possible for this edge to be a *forward edge*, in that
      // case the time won't be updated since time[v] < time[next]
      back[v] = min(back[v], time_in[next]);
    }
  }

  // the root vertex of the dfs tree is a cut-vertex
  // if it has more than two children in the dfs tree
  if (parent == -1 && children > 1) {
    is_cut_vertex = true;
  }

  if (is_cut_vertex) {
    cut_vertex.push_back(v);
  }
}

/**
 * Finds the articulation points in an undirected graph `G`
 * of order`n` and size `m`
 *
 * Time complexity: O(n + m)
 * Space complexity: O(n)
 *
 * @returns {int} the number of articulation points
 */
int articulation_points() {
  int n = g.size();
  time_spent = 0;
  time_in.assign(n, -1);
  back.assign(n, -1);
  cut_vertex.clear();

  for (int i = 0; i < n; i += 1) {
    if (time_in[i] == -1) {
      dfs(i, -1);
    }
  }
  return cut_vertex.size();
}

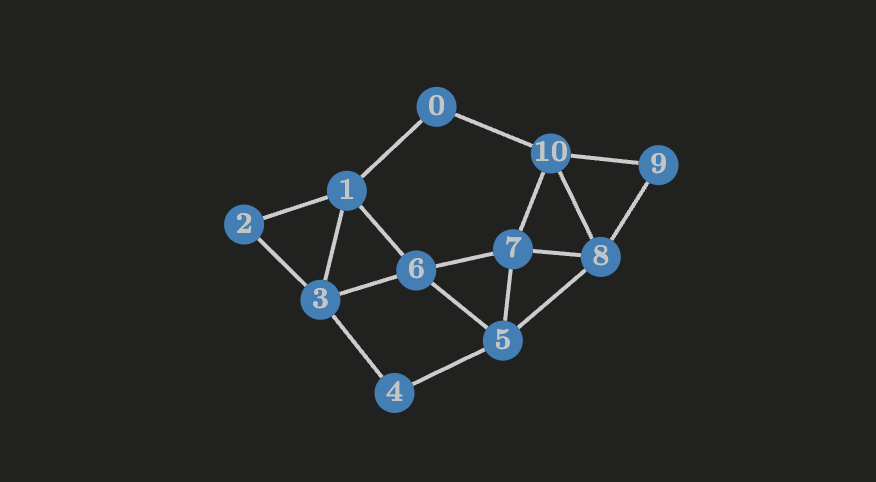
Biconnected components in an undirected graph

A biconnected graph is a nonseparable graph, meaning that if any vertex is removed, the graph is still connected, and therefore it doesn’t have cut-vertices.

Key observations:

• Two different biconnected components can’t have a common edge (but they might share a common vertex).
• A common vertex linking multiple biconnected components must be a cut-vertex of $G$.

Let $uv$ be an edge of an undirected graph $G$. We can keep a stack telling the order of the edges analyzed, so we push it to the stack. If $u$ is a cut-vertex, then all the edges from the top of the stack up to $uv$ are the edges of one biconnected component.

int time_spent;

// the adjacency list representation of `G`
vector<vector<int> > g;
// the time a vertex `i` was discovered first
vector<int> time_in;
// stores the discovery time of the lowest predecessor that vertex `i`'s
// succesor vertices can reach **through a back edge**, initially
// the lowest predecessor is set to the vertex itself
vector<int> back;

// the biconnected components found during the dfs
vector<vector<pair<int, int> > > bcc;
stack<pair<int, int> > edges_processed;

void output_biconnected_component(int u, int v) {
  pair<int, int> top;
  vector<pair<int, int> > component;
  do {
    top = edges_processed.top();
    edges_processed.pop();
    component.push_back(top);
  } while (u != top.first || v != top.second);
  bcc.push_back(component);
}

void dfs(int v, int parent) {
  // the lowest back edge discovery time of `v` is
  // set to the discovery time of `v` initally
  back[v] = time_in[v] = ++time_spent;

  // count the number of children for the `root` vertex
  int is_cut_vertex = false;

  for (int i = 0; i < g[v].size(); i += 1) {
    int next = g[v][i];

    if (parent == next) {
      continue;
    }

    // mark the edge (v, next) as processed
    if (time_in[next] == -1) {
      // this edge is being processed right now
      edges_processed.push(pair<int, int> (v, next));

      dfs(next, v);
      // if there's a back edge between a descendant of `next` and
      // a predecessor of `v` then `next` will have a lower reachable
      // vertex than `v` through a back edge, in this case the vertex `v` is not
      // a cut-vertex
      if (back[next] >= time_in[v]) {
        output_biconnected_component(v, next);
      }
      // propagation of the back edge to a vertex with the lowest discovery time
      back[v] = min(back[v], back[next]);
    } else if (time_in[next] < time_in[v]) {
      // * back edge *
      // update index of the vertex incident with this back edge to
      // be the one with the lowest discovery time
      back[v] = min(back[v], time_in[next]);

      // push this edge to the stack only once
      edges_processed.push(pair<int, int> (v, next));
    }
  }
}

/**
 * Finds the biconnected components in an undirected graph `G`
 * of order`n` and size `m`
 *
 * Time complexity: O(n + m)
 * Space complexity: O(m)
 *
 * @returns {int} the number of biconnected components
 */
int biconnected_components() {
  int n = g.size();
  time_spent = 0;
  time_in.assign(n, -1);
  back.assign(n, -1);

  while (!edges_processed.empty()) {
    edges_processed.pop();
  }
  bcc.clear();

  for (int i = 0; i < n; i += 1) {
    if (time_in[i] == -1) {
      dfs(i, -1);
    }
  }

  return bcc.size();
}

Connectivity

Let $G$ be a non-complete graph without cut-vertices. Let $U$ be a set of vertices of $G$ such that $G-U$ is disconnected. $U$ is called a vertex-cut set

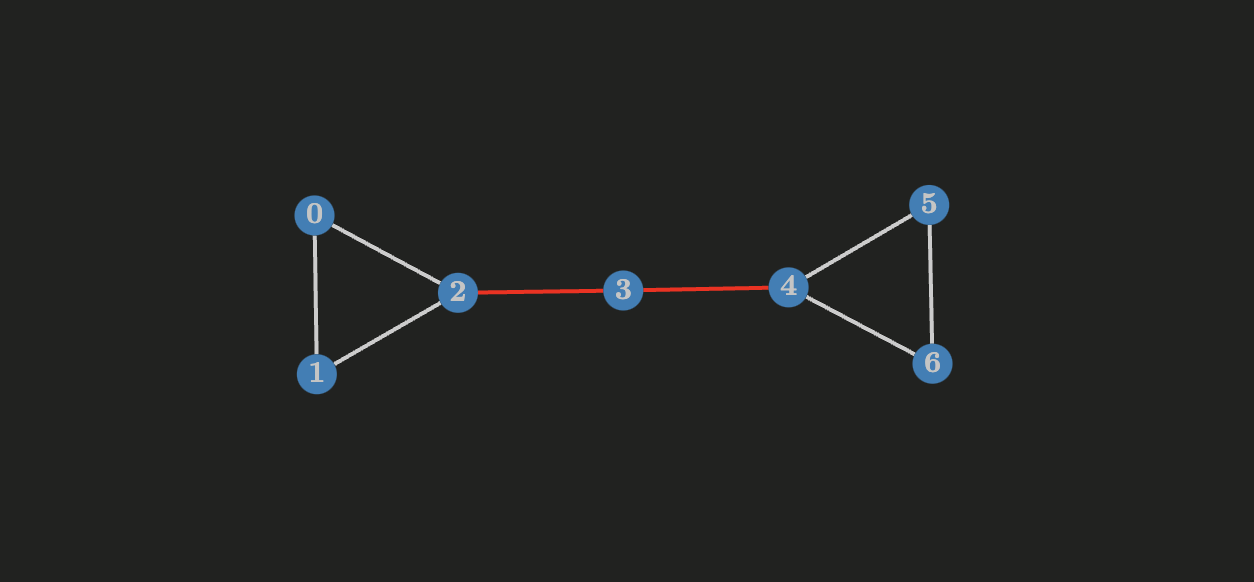
The graph below doesn’t have a cut-vertex, but it has many vertex-cut sets: $U_1=v_1,v_2$, $U_2=v_2,v_4$, $U_3=v_1,v_2,v_3$, $U_4=v_1,v_2,v_4$, $U_5=v_0,v_2,v_4$.

• The set with minimum cardinality is called a minimum vertex-cut set.
• A connected graph $G$ contains a cut-vertex set only if $G$ is not complete.

For a graph $G$ that is not complete, the vertex-connectivity, denoted as $\kappa (G)$, is the cardinality of the minimum vertex-cut set of $G$. For the graph above, $\kappa (G)=2$.

• If $G$ is a graph of order $n$ and size $m\ge n-1$, then $\kappa (G)=\lfloor \frac{2m}{n}\rfloor$.

There are other measures of how connected a graph is. Let $X$ be a set of edges of $G$ such that $G-X$ is disconnected or a trivial graph. $X$ is called an edge-cut set. The edge-connectivity, denoted as $\lambda (G)$, is the cardinality of the minimum edge-cut of $G$.

• For a complete graph $G$ of order $n$, $\lambda (G)=n-1$.