Undirected graph

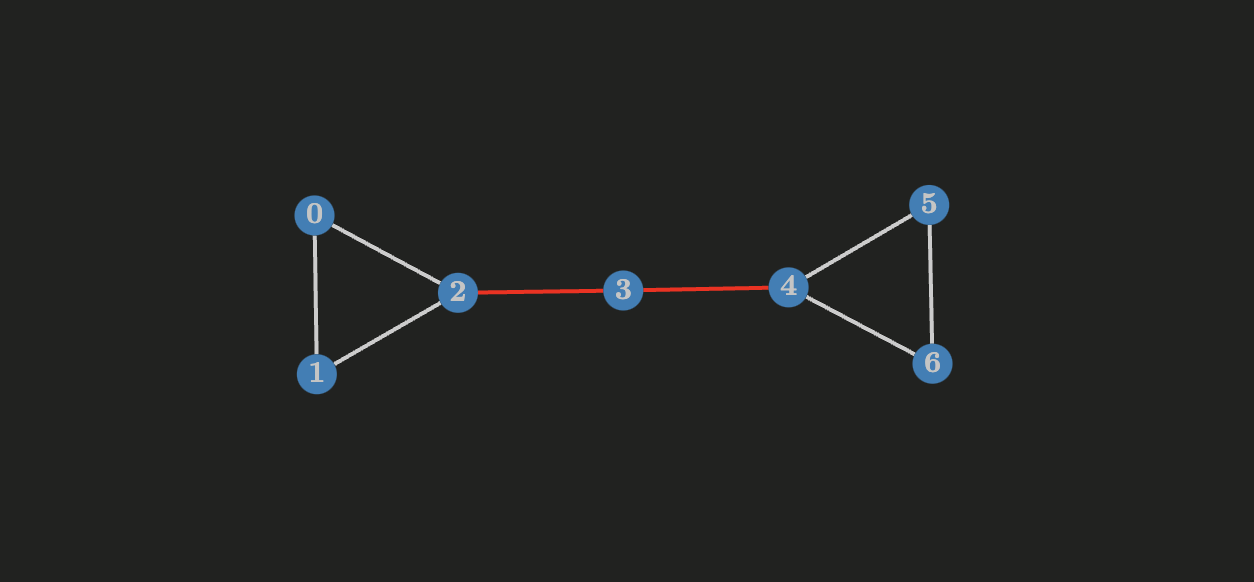
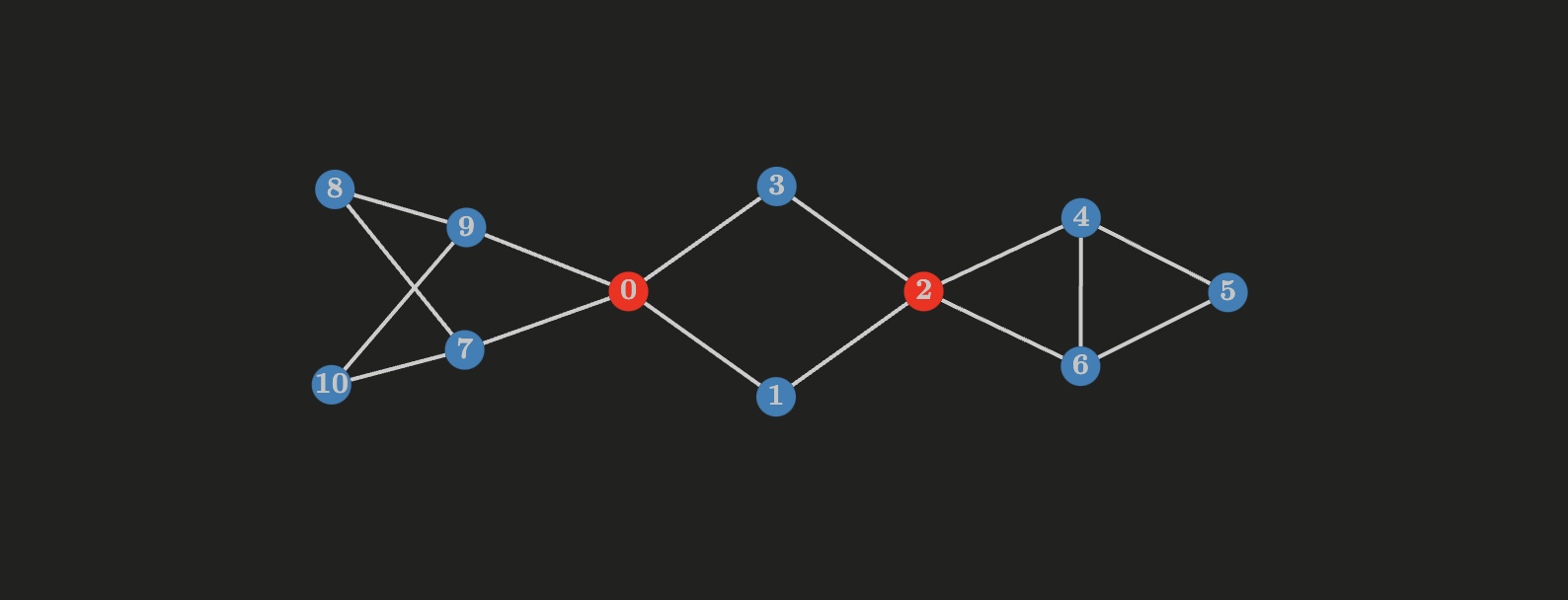
In the following undirected graph $G$, the edges $v_2{v}_3$ and $v_3{v}_4$ are bridges.

• An edge $e$ of an undirected graph $G$ is a bridge if and only if $e$ lies on no cycle of $G$.
• Every edge of an undirected tree is a bridge.

Let $G$ be an undirected graph. By analyzing the properties of the DFS tree, we can determine if an edge is a bridge given the following facts:

• Let $u$ and $v$ be two vertices of the DFS tree such that $u$ is an ancestor of $v$. Also, $u$ and $v$ are not adjacent.
  • If there’s a back edge $vu$, then none of the edges in the $u-v$ path are bridges. If we remove one of them, the graph is still connected because of this edge.
  • Otherwise, the edge is a bridge.

Implementation notes

• To check if a successor of a vertex $u$ has a back edge to a predecessor of $u$, an additional state is stored in each vertex, which is the discovery time of the lowest back edge of a successor of $u$ (by lowest back edge, we mean the back edge to a vertex with the lowest discovery time), denoted as $u_{back}$. Initially, this state is set to the discovery time of the vertex $v$, i.e., $u_{back}=u_{in}$. This state is propagated when backtracking is performed.
• Let $uv$ be a back edge. When this edge is analyzed, the $v_{back}$ state needs to be updated to be the minimum of the existing $v_{back}$ and the discovery time of $u$, i.e., $v_{back}=min(v_{back},u_{in})$.
• Let $v$ be an adjacent successor of $u$ in the DFS tree. When we’ve finished analyzing the branch of the tree because of the $uv$ edge, we have to check if the $v_{back}$ state contains a back edge to some predecessor of $u$ ($v_{back}$ is propagated), i.e., $u_{in}>v_{back}$. If so, then $uv$ is not a bridge.

int time_spent;

// the adjacency list representation of `G`
vector<vector<int> > g;
// the time a vertex `i` was discovered first
vector<int> time_in;
// stores the discovery time of the lowest predecessor that vertex `i`'s
// succesor vertices can reach **through a back edge**, initially
// the lowest predecessor is set to the vertex itself
vector<int> back;
// the bridges found during the dfs
vector<pair<int, int> > cut_edge;

void dfs(int v, int parent) {
  // the lowest back edge discovery time of `v` is
  // set to the discovery time of `v` initally
  back[v] = time_in[v] = ++time_spent;

  for (int i = 0; i < g[v].size(); i += 1) {
    int next = g[v][i];

    if (next == parent) {
      continue;
    }

    if (time_in[next] == -1) {
      dfs(next, v);
      // if there's a back edge between a descendant of `next` and
      // a predecessor of `v` then `next` will have a lower back edge discovery time
      // otherwise it's a bridge
      if (back[next] > time_in[v]) {
        cut_edge.push_back(pair<int, int> (v, next));
      }
      // propagation of the lowest back edge discovery time
      back[v] = min(back[v], back[next]);
    } else {
      // *back edge*
      // update the lowest back edge discovery time of `v`
      back[v] = min(back[v], time_in[next]);
    }
  }
}

/**
 * Finds the bridges in an undirected graph `G` of order `n` and size `m`
 *
 * Time complexity: O(n + m)
 * Space complexity: O(n)
 */
void bridges() {
  int n = g.size();
  time_spent = 0;
  time_in.assign(n, -1);
  back.assign(n, -1);
  cut_edge.clear();

  for (int i = 0; i < n; i += 1) {
    if (time_in[i] == -1) {
      dfs(i, -1);
    }
  }
}

Directed graph (strong bridges)

Let $G$ be a directed graph. An edge $uv\in E(G)$ is a strong bridge if its removal increases the number of strongly connected components of $G$.

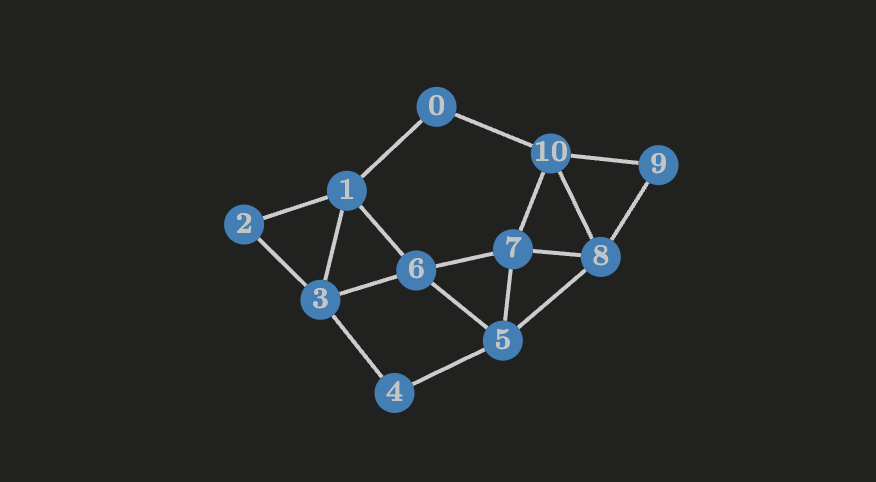
The following is a connected graph $G$. Every edge but $v_2{v}_0$ is a strong bridge because removing it from $G$ increases the number of strongly connected components. Removing $v_2{v}_0$ doesn’t increase the number of strongly connected components, so it’s not a bridge.

A trivial algorithm to find the strong bridges of a digraph $G$ of order $n$ and size $m$ is as follows:

• Compute the number of strongly connected components of $G$, denoted as $k(G)$.
• For each edge $e\in E(G)$:
• remove $e$ from $G$
• compute the number of strongly connected components of $G$, denoted as $k(G-e)$
• if $k(G)<k(G-e)$, then $e$ is a bridge.

The time complexity of the algorithm above is clearly $O(m(n+m))$.

Let $uv$ be an edge of a digraph $G$. We say that $uv$ is redundant if there’s an alternative path from vertex $u$ to vertex $v$ avoiding $uv$. Otherwise, we say that $uv$ is not redundant. Computing the strong bridges is equivalent to computing the non-redundant edges of a graph.

http://www.sofsem.cz/sofsem12/files/presentations/Thursday/GiuseppeItaliano.pdf