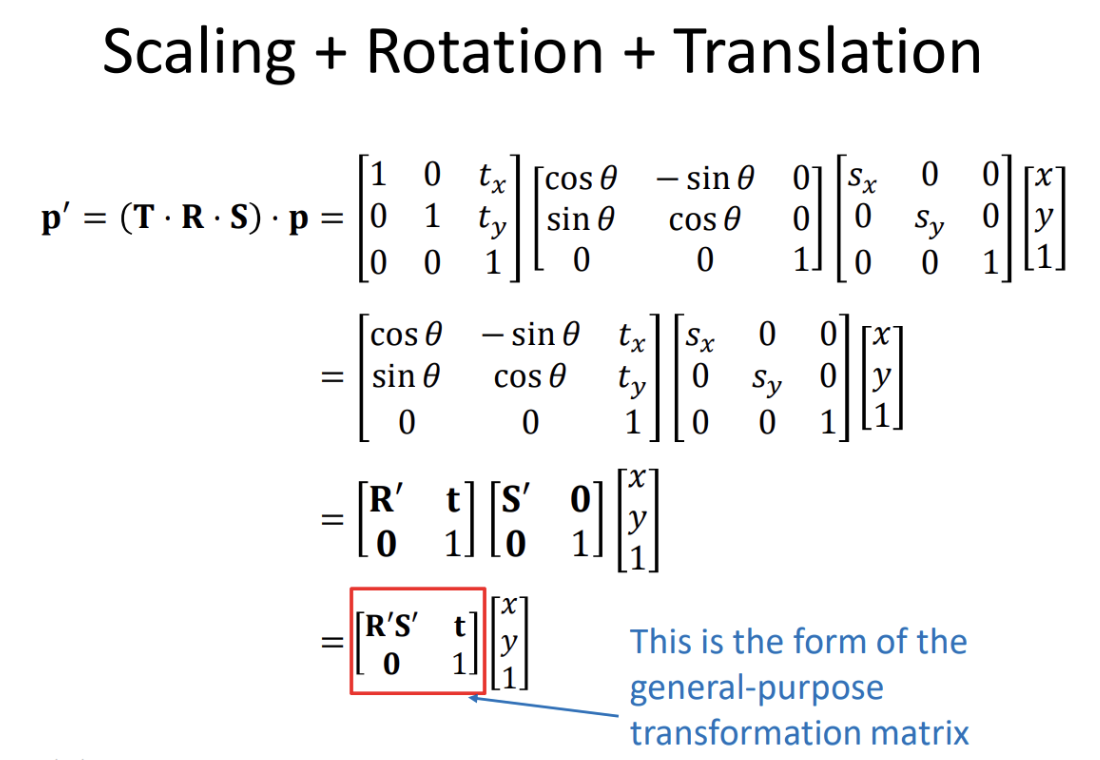
A first-person camera captures objects from the viewpoint of a player’s character. The camera has the following characteristics:

• Orbit: The character can look left, right, up, and down; however, if we imagine the character’s head, it can’t be tilted.
• Translation: The character can move in four directions: forward, backward, left, and right. Note that the vector that represents the direction the character is looking at doesn’t change (the orbit is not affected by translation).
  • Our camera will always move in the same direction the camera is looking. This is usually done differently in first-person shooters, where the character may move in a different direction than the camera is looking.

Both characteristics can be implemented by creating a space for the camera and defining the direction in this space. That way, translation doesn’t modify the direction the camera is looking at, and for orbit, we would rotate the basis vectors of the space.

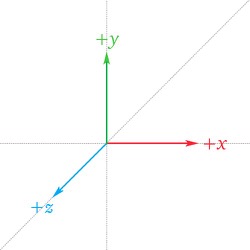
Assuming that the world space axes are as follows:

Let $\mathbf{M}{upright \leftarrow camera}$ be the rotation matrix that transforms points from camera space to upright space. Also, let the “look at” vector be defined as $\mathbf{p}{camera} = $$\left[\begin{array}{ccc}0& 0& -1\end{array}\right]$$^T$ in camera space. To define the rotation matrix ${\mathbf{M}}_{upright\leftarrow camera}$, let’s first identify the Euler angles involved in the rotation. Taking the image above as a reference, we can identify the following actions:

• The character looks left or right - rotation relative to the upright space $y$-axis.
• The character looks up or down - rotation relative to the upright space $x$-axis.

Note that the sequence of intrinsic rotations ($y-x^{\prime }$ or $x-y$ if expressed as a sequence of extrinsic rotations) represents the rotation of the camera. The sequence of extrinsic rotations can be represented as a multiplication of the following rotation matrices:

The angles $\alpha$ and $\beta$ are computed as follows:

• Let $\mathrm{\Delta }\alpha$ and $\mathrm{\Delta }\beta$ represent the change in the rotation around the $\mathbf{Y}$ and $\mathbf{X}$ axes, respectively. The values of $\alpha$ and $\beta$ are computed based on the previous state:

• If the character looks up, then $\mathrm{\Delta }\beta$ is positive.
• If the character looks to the right, then $\mathrm{\Delta }\alpha$ is negative.

Mouse Coordinates Delta to Extrinsic Rotations Delta

Next, we need to define what happens when we move the mouse. We can configure a window manager like GLFW to call a callback method whenever we move the mouse with the coordinates of the mouse as an argument (e.g., as $x_{new}$ and $y_{new}$). Note: The coordinates of the mouse are expressed relative to the top-left corner of the window, whose $+x$-axis points right and $+y$-axis points down. If we keep the old coordinates of the mouse (as $x_{old}$ and $y_{old}$), we can obtain how much the mouse moved with respect to the old position with the following calculation:

Note that $y_{new}-y_{old}$ will be positive if we move the mouse down, which is unintuitive. Therefore, we can multiply this result by $-1$ so that moving the mouse downward sets a negative value in $\mathrm{\Delta }y$.

The next step is to update the values of $\alpha$ (yaw) and $\beta$ (pitch) using $\mathrm{\Delta }x$ and $\mathrm{\Delta }y$. Note that when we move the mouse to the right, we’re moving clockwise with respect to the $+y$-axis, and when we move the mouse upward, we’re moving counterclockwise with respect to the $+x$-axis. Therefore:

Note that we also need the value of $\beta$ to be inside the range $-{90}^{°}\le \beta \le {90}^{°}$ to avoid looking backward.

Finally, to compute the value of $\mathbf{p}{world}$,weneedtotransform$\mathbf{p}{object}$with$\mathbf{M}{world \leftarrow object}$.Notethatthevalueof$\mathbf{p}{object} = $$\left[\begin{array}{ccc}0& 0& -1\end{array}\right]$$^T$isalwaysthesame.Therefore,thevalueof$\mathbf{p}_{world}$ is:

#pragma once

class FPS_Mouse {
public:
  float sensitivity;
  float yaw
  float pitch;
  glm::vec4 target;

  static const glm::vec3 YAW_AXIS = glm::vec3(0.0f, 1.0f, 0.0f);
  static const glm::vec3 PITCH_AXIS = glm::vec3(1.0f, 0.0f, 0.0f);

  FPS_Mouse(float yaw, float pitch);
  void process_mouse_movement(double delta_x, double delta_y, bool constraint_pitch);
  glm::mat4 get_view_matrix() const;

private:
  static const glm::vec4 P = glm::vec3(0.0f, 0.0f, -1.0f, 1.0f);
  void update_target();
}

FPS_Mouse::FPS_Mouse(float yaw = 0, float pitch = 0) :
    sensitivity(0.05f) {
  this->yaw = yaw;
  this->pitch = pitch;
  this->update_target();
}

void FPS_Mouse::process_mouse_movement(double delta_x, double delta_y, bool constraint_pitch = true) {
  yaw -= delta_x * sensitivity;
  pitch += delta_y * sensitivity;

  if (constraint_pitch) {
    if (pitch > 89.0f) { pitch = 89.0f; }
    if (pitch < -89.0f) { pitch = -89.0f; }
  } 
  this->update_target();
}

void FPS_Mouse::update_target() {
  /* Y = glm::rotate(glm::mat4(1.0f), glm::radians(yaw), FPS::YAW_AXIS); */
  /* X = glm::rotate(glm::mat4(1.0f), glm::radians(pitch), FPS::PITCH_AXIS); */
  /* target = Y * X * p; */
  float yaw_radians = glm::radians(yaw);
  float pitch_radians = glm::radians(pitch);
  target.x = -sin(yaw_radians) * cos(pitch_radians);
  target.y = sin(pitch_radians);
  target.z = -cos(yaw_radians) * cos(pitch_radians);
}