Many objects will have a surface that is not shiny for example wood and paper, such objects can be modeled using the Lambertian Model

Lambertian shading model

A Lambertian object obeys the Lambert’s cosine law which states that

The luminous intensity of a surface is proportional to the cosine of the angle between the surface normal and the direction of the light

$$c\propto \cos \theta \text{or}c\propto \mathbf{n}\cdot \mathbf{l}$$

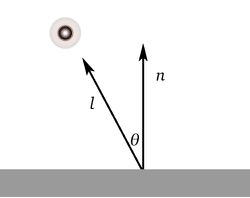
Note that the model does not depend on the distance between the light and the object, this assumption is equivalent to saying that the light is “distant” relative to the object size which is often a directional light

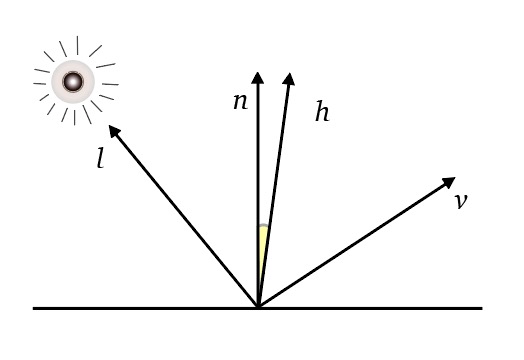
When the light hits the surface a portion of the light gets reflected, this is controlled by the diffuse reflectance $c_r$, a color that varies depending on the surface, also the surface color can be made darker/lighter by changing the color of the light source $c_l$

$c_r$ and $c_l$ are RGB colors with components in the range $[0,1]$ where the multiplication is done element-wise so $c_r;c_l$ returns another RGB color, note however that the product $\mathbf{n}\cdot \mathbf{l}$ might create negative values (e.g. when the surface normal is pointing away from the light), to solve this we can use the max function

Ambient shading

Some surfaces that receive no direct illumination in real life are perceived as having a color distinct to black, this is because the light is actually reflected in other surfaces. In addition there’s sometimes skylight which increases the amount of light reflected

A common trick is to put a dim light at the position of the eye so that all visible points receive some light, another approach is to add an ambient color $c_a$ which is simply a constant value which interacts with the diffuse reflectance $c_r$